K-veïns més propers (KNN)
- Introducció
- Aprenentatge basat en instàncies vs basats en models
- Exemple pràctic amb KNN
- Com funciona KNN?
- L’algoritme KNN pas a pas
- Escollir el valor de K
- Mètriques de distància
- Importància de l’escalat de característiques
- KNN per a regressió
- La maledicció de la dimensionalitat
- Avantatges i desavantatges de KNN
- Implementació amb Python
- KNN vs Arbres de Decisió
- Resum
Introducció
Després d’estudiar els arbres de decisió, que construeixen un model explícit a partir de les dades d’entrenament, ara veurem un algoritme radicalment diferent: K-Veïns Més Propers (KNN o K-Nearest Neighbors).
La idea de KNN és molt simple i intuïtiva:
Per classificar un nou exemple, mira quins són els exemples d’entrenament més semblants i assigna-li la mateixa etiqueta que la majoria d’aquests veïns.
Aprenentatge basat en instàncies vs basats en models
Abans de veure com funciona KNN, és important entendre una distinció fonamental en machine learning:
Algoritmes basats en models (Model-based Learning)
Els algoritmes basats en models, com els arbres de decisió o les xarxes neuronals, funcionen en dues fases ben diferenciades:
-
Fase d’entrenament:
- Processen les dades d’entrenament
- Construeixen un model explícit (un arbre, uns pesos, etc.)
- Un cop entrenat, poden descartar les dades d’entrenament
-
Fase de predicció:
- Només utilitzen el model construït
- Són ràpids perquè el model és compacte
Exemple: Un arbre de decisió amb 1000 exemples d’entrenament pot acabar sent un arbre amb només 20 nodes. Per fer una predicció, només cal recórrer l’arbre (molt ràpid).
Algoritmes basats en instàncies (Instance-based Learning)
Els algoritmes basats en instàncies, com KNN, funcionen de manera totalment diferent:
-
Fase d’entrenament:
- Només emmagatzemen les dades
- No construeixen cap model explícit
- També s’anomenen lazy learners (aprenents mandrosos)
-
Fase de predicció:
- Comparen el nou exemple amb TOTES les dades emmagatzemades
- Són lents perquè han de consultar tota la base de dades
Exemple: KNN amb 1000 exemples d’entrenament ha de calcular 1000 distàncies per cada predicció.
Comparació visual
| Aspecte | Model-based (Arbres) | Instance-based (KNN) |
|---|---|---|
| Entrenament | Lent (construeix model) | Instantani (només emmagatzema) |
| Predicció | Ràpid (consulta model) | Lent (cerca en totes les dades) |
| Memòria | Baixa (només el model) | Alta (totes les dades) |
| Analogia | Estudiar i fer un resum | Portar tots els apunts a l’examen |
Exemple pràctic amb KNN
Exemple: Classificació de fruites
Suposem que volem classificar taronges i llimones basant-nos en dues característiques:
- Pes (en grams)
- Grau de dolçor (en una escala de 0 a 10)
Disposem de 10 exemples d’entrenament: 5 taronges i 5 llimones.
Podem visualitzar aquestes dades en un gràfic de dispersió:
- Eix X: Pes (grams)
- Eix Y: Dolçor
- Taronges: punts taronges
- Llimones: punts grocs
Ara arriba una nova fruita amb:
- Pes = 150g
- Dolçor = 6
És una taronja o una llimona?
Com funciona KNN?
L’algoritme KNN segueix aquests passos:
Pas 1: Calcular distàncies
Primer, calculem la distància entre el nou exemple i tots els exemples d’entrenament.
La distància més habitual és la distància euclidiana:
d(x,x′)=√(x1−x′1)2+(x2−x′2)2
On:
- x=(x1,x2) és el nou exemple
- x′=(x′1,x′2) és un exemple d’entrenament
Per exemple, si el nou punt té coordenades (150, 6) i un exemple d’entrenament té (158, 6.5):
d=√(158−150)2+(6.5−6)2=√64+0.25=√64.25≈8.02
Pas 2: Seleccionar els K veïns més propers
Un cop tenim les distàncies a tots els exemples d’entrenament, ordenem els exemples per distància i seleccionem els K més propers.
Per exemple, si K=3, seleccionem els 3 exemples amb menor distància.
Pas 3: Votació
Finalment, mirem les etiquetes dels K veïns seleccionats i fem una votació majoritària:
- Si la majoria són taronges → predim taronja
- Si la majoria són llimones → predim llimona
Exemple amb K=3:
- Veí 1: taronja (distància 8.0)
- Veí 2: taronja (distància 10.0)
- Veí 3: llimona (distància 12.0)
Resultat de la votació:
- Taronja: 2 vots
- Llimona: 1 vot
Predicció final: Taronja
L’algoritme KNN pas a pas
Formalment, l’algoritme KNN per a classificació és:
Entrades:
- Conjunt d’entrenament: (x(1),y(1)),(x(2),y(2)),…,(x(m),y(m))
- Nou exemple a classificar: xnou
- Valor de K (nombre de veïns)
Procés:
-
Per cada exemple d’entrenament i=1,2,…,m:
- Calcula la distància di=d(xnou,x(i))
-
Ordena els exemples d’entrenament per distància creixent
-
Selecciona els K exemples amb menor distància
-
Compte el nombre de cada classe entre aquests K veïns
-
Retorna la classe amb més vots
Sortida:
- Predicció ˆy per al nou exemple
Pseudocodi
def knn_classify(X_train, y_train, x_new, K):
# 1. Calcular totes les distàncies
distances = []
for i in range(len(X_train)):
dist = euclidean_distance(x_new, X_train[i])
distances.append((dist, y_train[i]))
# 2. Ordenar per distància
distances.sort(key=lambda x: x[0])
# 3. Seleccionar els K més propers
k_nearest = distances[:K]
# 4. Votació majoritària
votes = {}
for _, label in k_nearest:
votes[label] = votes.get(label, 0) + 1
# 5. Retornar la classe més votada
return max(votes, key=votes.get)
Escollir el valor de K
Una de les decisions més importants en KNN és quant val K.
K massa petit (K=1)
Si K=1, només mirem el veí més proper. Això pot ser problemàtic:
- Molt sensible al soroll: si hi ha un exemple mal etiquetat, pot donar prediccions incorrectes
- Alta variància: petits canvis en les dades d’entrenament canvien molt les prediccions
- Fronteres de decisió irregulars i fragmentades: cada punt d’entrenament crea la seva pròpia “illa” de decisió
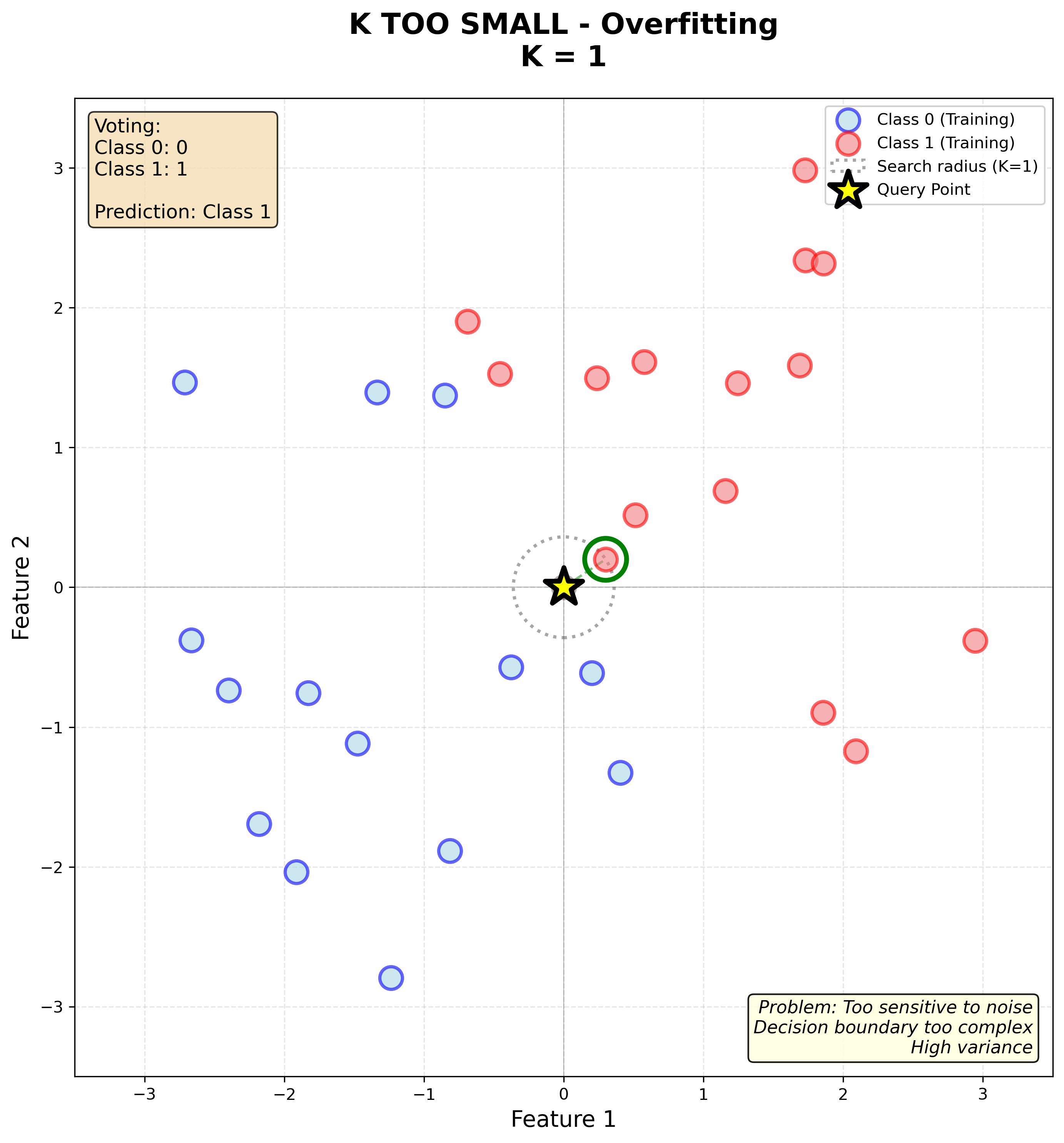
Observa en la gràfica com la frontera de decisió és molt irregular i fragmentada, amb zones petites al voltant de cada punt d’entrenament. Això indica overfitting: el model s’ajusta massa a les dades d’entrenament i no generalitzarà bé.
K massa gran (K=50, tots els punts)
Si K és molt gran (per exemple, igual al nombre total d’exemples):
- Sempre predirà la classe majoritària del conjunt d’entrenament
- Alta bias: el model és massa simple i no captura la complexitat de les dades
- Perd informació local: punts llunyans influeixen en la decisió com si fossin propers
- Frontera de decisió massa suau i lineal
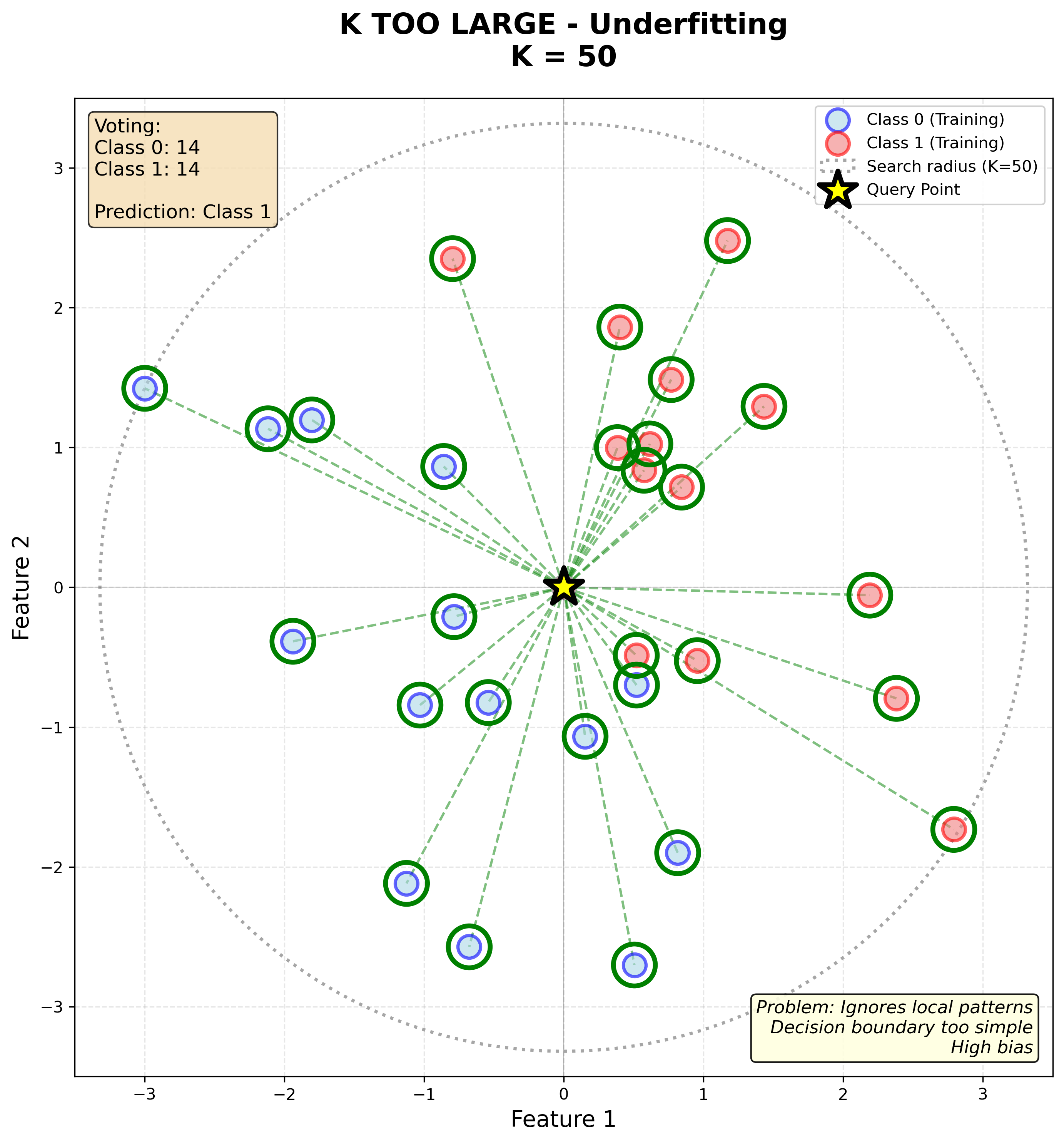
Observa com la frontera és ara molt suau i gairebé lineal, ignorant la distribució real dels punts. Això indica underfitting: el model és massa simple.
K òptim (K=11)
Un valor intermedi de K sol funcionar millor:
- Reducció del soroll: més robust que K=1 perquè diversos veïns voten
- Manté informació local: millor que K massa gran perquè només els veïns propers influeixen
- Frontera equilibrada: prou suau per generalitzar, però prou flexible per capturar la forma real de les dades
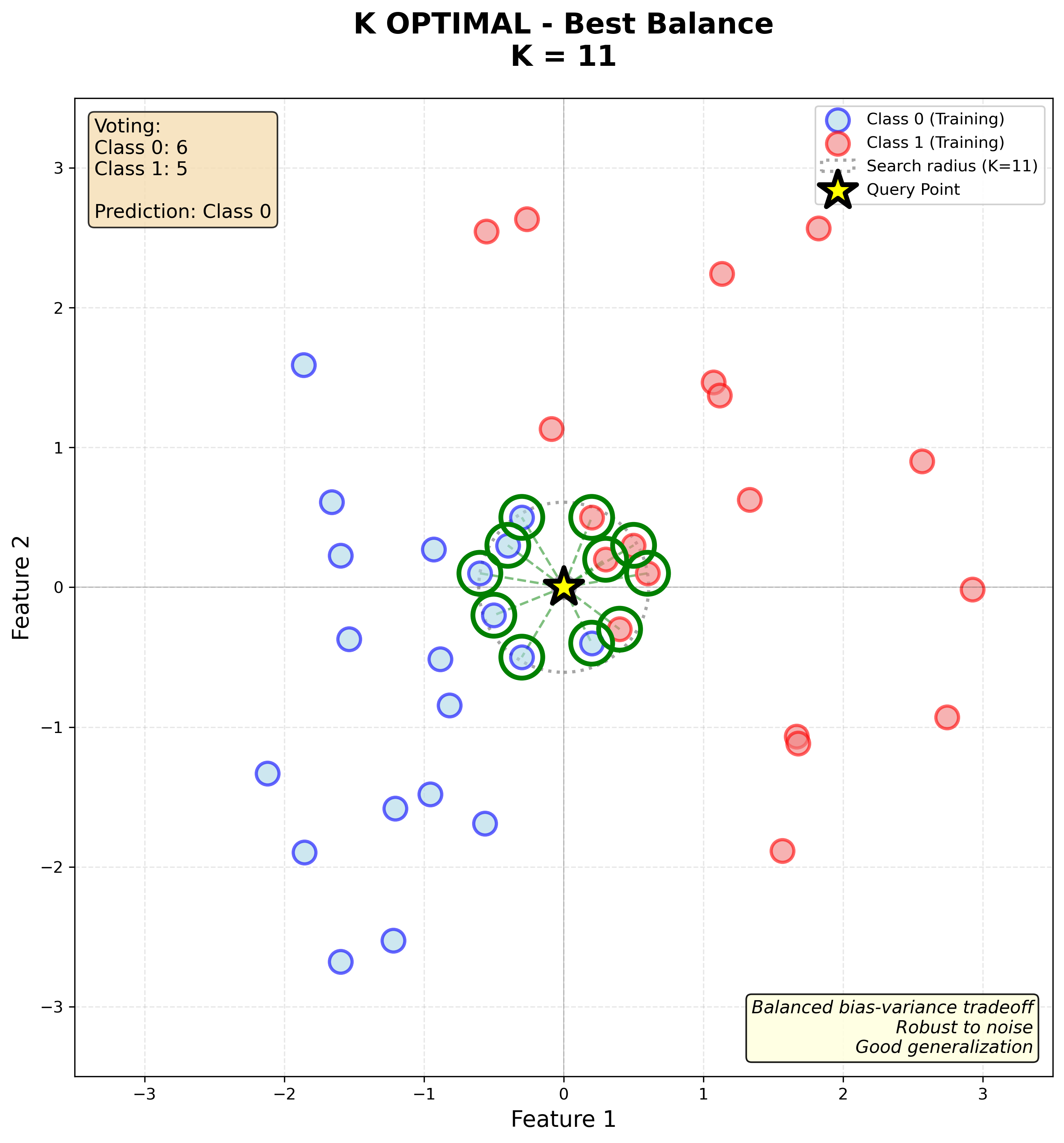
Observa com la frontera és més suau que amb K=1 però encara respecta la distribució dels punts, creant una separació natural entre taronges i llimones. Aquest és el compromís òptim entre bias i variància.
Recomanacions pràctiques:
- Començar amb K=√m, on m és el nombre d’exemples d’entrenament
- Utilitzar validació creuada per trobar el millor K
- Preferir valors imparells de K per evitar empats en classificació binària
Trobar K amb validació creuada
El procés típic és:
- Provar diferents valors de K: per exemple, K=1,3,5,7,9,11,…
- Per a cada valor de K:
- Entrenar el model amb el conjunt d’entrenament
- Avaluar-lo amb el conjunt de validació
- Calcular l’error de validació
- Escollir el K amb menor error de validació
- Avaluar el model final amb el conjunt de test
La gràfica mostra com l’error de validació varia amb K:
- Per K petit: overfitting (alta variància)
- Per K gran: underfitting (alta bias)
- El mínim indica el millor valor de K
Mètriques de distància
La distància euclidiana no és l’única opció. Depenent del problema, altres mètriques poden funcionar millor.
Distància euclidiana
És la distància “en línia recta” en l’espai euclidià:
deuclidiana(x,x′)=√n∑i=1(xi−x′i)2
- Avantatge: intuïtiva, funciona bé en molts casos
- Desavantatge: sensible a l’escala de les característiques
Distància de Manhattan
També anomenada distància L1 o city-block distance:
dManhattan(x,x′)=n∑i=1|xi−x′i|
Mesura la distància com si es caminés per carrers en una quadrícula.
- Avantatge: menys sensible a outliers que l’euclidiana
- Ús: funciona bé en espais d’alta dimensió
Distància de Minkowski
Una generalització de les anteriors:
dMinkowski(x,x′)=(n∑i=1|xi−x′i|p)1/p
On:
- p=1: distància de Manhattan
- p=2: distància euclidiana
- p=∞: distància de Chebyshev (max)
Comparació visual
Quan usar cada mètrica?
| Mètrica | Millor per a |
|---|---|
| Euclidiana | Dades contínues, característiques amb unitats similars |
| Manhattan | Dades d’alta dimensió, presència d’outliers |
| Cosine | Dades de text (vectors de paraules), direcció més important que magnitud |
Importància de l’escalat de característiques
Un problema important de KNN és que és molt sensible a l’escala de les característiques.
Exemple problemàtic
Imaginem que volem classificar cases en “cares” o “barates” basant-nos en:
- Característica 1: Superfície (en m²) → rang [50, 300]
- Característica 2: Nombre d’habitacions → rang [1, 5]
Si calculem la distància euclidiana sense normalitzar:
d = \sqrt{(200 - 150)^2 + (3 - 2)^2} = \sqrt{2500 + 1} = \sqrt{2501} \approx 50
La característica de superfície domina el càlcul perquè els seus valors són molt més grans!
Solució: Normalització
Hem d’escalar totes les característiques a un rang similar.
Min-Max Scaling
Escala els valors a l’interval [0, 1]:
x’_i = \frac{x_i - \min(x)}{\max(x) - \min(x)}
Standardització (Z-score)
Transforma les dades per tenir mitjana 0 i desviació estàndard 1:
x’_i = \frac{x_i - \mu}{\sigma}
On:
- \mu és la mitjana
- \sigma és la desviació estàndard
Exemple pràctic
Abans de normalitzar:
| Casa | Superfície (m²) | Habitacions | Preu |
|---|---|---|---|
| 1 | 100 | 2 | Barat |
| 2 | 200 | 4 | Car |
Després de min-max scaling:
| Casa | Superfície | Habitacions | Preu |
|---|---|---|---|
| 1 | 0.0 | 0.0 | Barat |
| 2 | 1.0 | 1.0 | Car |
Ara ambdues característiques tenen el mateix pes en el càlcul de distàncies.
KNN per a regressió
KNN no només serveix per a classificació. També podem utilitzar-lo per regressió, és a dir, per predir valors numèrics.
Diferència clau
En lloc de fer una votació majoritària, calculem la mitjana dels valors dels K veïns més propers.
Algoritme KNN per regressió
Procés:
- Calcular distàncies a tots els exemples d’entrenament
- Seleccionar els K veïns més propers
- Calcular la mitjana dels valors y d’aquests veïns
- Retornar aquesta mitjana com a predicció
Formalment:
\hat{y} = \frac{1}{K} \sum_{i \in \text{K-veïns}} y^{(i)}
Exemple: Predir el preu d’un habitatge
Suposem que volem predir el preu d’un habitatge basant-nos en la seva superfície.
Conjunt d’entrenament:
| Superfície (m²) | Preu (k€) |
|---|---|
| 50 | 100 |
| 80 | 150 |
| 100 | 180 |
| 120 | 200 |
| 150 | 250 |
Nova casa: 90 m²
Amb K = 3, els 3 veïns més propers són:
| Superfície | Preu | Distància |
|---|---|---|
| 80 | 150 | 10 |
| 100 | 180 | 10 |
| 50 | 100 | 40 |
Predicció:
\hat{y} = \frac{150 + 180 + 100}{3} = \frac{430}{3} \approx 143.3 \text{ k€}
Variació: Mitjana ponderada
En lloc d’una mitjana simple, podem donar més pes als veïns més propers:
\hat{y} = \frac{\sum_{i \in \text{K-veïns}} w_i \cdot y^{(i)}}{\sum_{i \in \text{K-veïns}} w_i}
On el pes pot ser:
w_i = \frac{1}{d_i}
(inversament proporcional a la distància)
Exemples més propers tenen més influència en la predicció.
La maledicció de la dimensionalitat
Un dels problemes més importants de KNN és la maledicció de la dimensionalitat (curse of dimensionality).
Què és?
Quan el nombre de característiques (dimensions) augmenta, passa alguna cosa sorprenent:
Tots els punts es tornen aproximadament equidistants entre si.
Això fa que el concepte de “veí més proper” perdi significat.
Exemple intuïtiu
Imaginem que tenim punts distribuïts aleatòriament en un hiperespai:
- 1D (una línia): És fàcil trobar punts propers
- 2D (un pla): Encara funciona bé
- 3D (un cub): Comença a complicar-se
- 100D: Tots els punts estan aproximadament a la mateixa distància!
Per què passa?
En dimensions altes:
- El volum de l’espai creix exponencialment
- Els punts es dispersen molt
- La distància entre el veí més proper i el més llunyà convergeix
Matemàticament, la ràtio:
\frac{d_{\max} - d_{\min}}{d_{\min}} \to 0 \quad \text{quan } n \to \infty
Conseqüències per KNN
- Necessitem moltes més dades en dimensions altes
- Les prediccions es tornen menys fiables
- El temps de càlcul augmenta (hem de calcular distàncies en més dimensions)
Solucions
-
Reducció de dimensionalitat:
- PCA (Principal Component Analysis)
- Feature selection (seleccionar només les característiques més rellevants)
-
Regularització: Penalitzar característiques poc informatives
-
Usar altres algoritmes: En dimensions molt altes, arbres de decisió o xarxes neuronals poden funcionar millor
Avantatges i desavantatges de KNN
Avantatges
-
Molt simple d’entendre i implementar
- No requereix matemàtiques avançades
- Codi molt curt
-
No necessita entrenament
- És un algoritme “lazy” (mandrós)
- Només emmagatzema les dades
-
Funciona bé amb dades no lineals
- No assumeix cap distribució de les dades
- Fronteres de decisió flexibles
-
Pot fer tant classificació com regressió
- Mateix algoritme, només canvia l’agregació final
-
Adaptable a nous exemples
- Només cal afegir nous punts al conjunt d’entrenament
Desavantatges
-
Computacionalment costós per a prediccions
- Cada predicció costa O(m \cdot n)
- On m = nombre d’exemples, n = nombre de dimensions
- Per grans datasets, és molt lent
-
Requereix molta memòria
- Ha d’emmagatzemar tot el conjunt d’entrenament
- Problemàtic amb datasets grans
-
Sensible a l’escala de les característiques
- Sempre cal normalitzar les dades
-
Sensible al soroll i outliers
- Un exemple mal etiquetat pot afectar les prediccions
-
Maledicció de la dimensionalitat
- No funciona bé amb moltes característiques
- Necessita moltes dades en dimensions altes
-
Difícil amb característiques categòriques
- Necessita mètriques de distància adaptades
Implementació amb Python
A continuació veurem com implementar KNN amb la biblioteca scikit-learn.
Classificació amb KNN
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
# 1. Preparar les dades
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# 2. Normalitzar les característiques (IMPORTANT!)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 3. Crear i entrenar el model KNN
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train_scaled, y_train)
# 4. Fer prediccions
y_pred = knn.predict(X_test_scaled)
# 5. Avaluar
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2%}")
print("\nClassification Report:")
print(classification_report(y_test, y_pred))
Regressió amb KNN
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
# Crear i entrenar el model per regressió
knn_reg = KNeighborsRegressor(n_neighbors=5)
knn_reg.fit(X_train_scaled, y_train)
# Fer prediccions
y_pred = knn_reg.predict(X_test_scaled)
# Avaluar amb múltiples mètriques
mse = mean_squared_error(y_test, y_pred)
rmse = mean_squared_error(y_test, y_pred, squared=False)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"MSE: {mse:.2f}")
print(f"RMSE: {rmse:.2f}")
print(f"MAE: {mae:.2f}")
print(f"R²: {r2:.2f}")
Trobar el millor K
from sklearn.model_selection import GridSearchCV
# Definir el rang de valors de K a provar
param_grid = {
'n_neighbors': [1, 3, 5, 7, 9, 11, 15, 21],
'weights': ['uniform', 'distance'],
'metric': ['euclidean', 'manhattan']
}
# Crear el model base
knn = KNeighborsClassifier()
# Cerca exhaustiva amb validació creuada
grid_search = GridSearchCV(
knn, param_grid, cv=5, scoring='accuracy', n_jobs=-1, verbose=1
)
grid_search.fit(X_train_scaled, y_train)
# Millors hiperparàmetres
print(f"Millors hiperparàmetres: {grid_search.best_params_}")
print(f"Millor accuracy (CV): {grid_search.best_score_:.2%}")
# Usar el millor model
best_knn = grid_search.best_estimator_
y_pred = best_knn.predict(X_test_scaled)
test_accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy en test: {test_accuracy:.2%}")
Opcions addicionals
# Usar distància de Manhattan
knn = KNeighborsClassifier(n_neighbors=5, metric='manhattan')
# Usar pesos basats en distància
knn = KNeighborsClassifier(n_neighbors=5, weights='distance')
# Especificar l'algoritme de cerca de veïns
knn = KNeighborsClassifier(n_neighbors=5, algorithm='ball_tree')
KNN vs Arbres de Decisió
Ara que hem vist tant KNN com arbres de decisió, fem una comparació:
| Aspecte | KNN | Arbres de Decisió |
|---|---|---|
| Tipus | Instance-based (lazy) | Model-based |
| Entrenament | Instant (només emmagatzema) | Pot trigar (construeix model) |
| Predicció | Lent (O(m \cdot n)) | Ràpid (O(\log m)) |
| Memòria | Alta (tot el dataset) | Baixa (només l’arbre) |
| Interpretabilitat | Difícil | Fàcil (arbres petits) |
| Fronteres de decisió | Suaus, no lineals | Rectangulars, ortogonals |
| Normalització | Imprescindible | No necessària |
| Alta dimensionalitat | Problemàtic | Funciona bé |
| Soroll | Sensible | Menys sensible (amb ensembles) |
| Característiques categòriques | Requereix codificació especial | Maneja directament |
Quan usar KNN?
- Datasets petits o mitjans (< 10,000 exemples)
- Poques dimensions (< 20 característiques)
- Dades amb fronteres de decisió complexes
- Quan no cal interpretabilitat
- Quan el temps de predicció no és crític
Quan usar arbres de decisió?
- Datasets grans
- Moltes dimensions
- Quan necessitem prediccions ràpides
- Quan volem interpretabilitat
- Dades tabulars amb característiques mixtes (categòriques + contínues)
- Quan hi ha soroll (usar ensembles com Random Forest o XGBoost)
Resum
-
KNN és un algoritme d’aprenentatge instance-based que classifica nous exemples basant-se en la similitud amb exemples d’entrenament.
-
El valor de K és crític:
- K petit → alta variància, sensible al soroll
- K gran → alta bias, perd informació local
- Trobar amb validació creuada
-
Distàncies: Euclidiana, Manhattan, Minkowski, etc.
- La tria depèn del problema
-
Escalat de característiques és imprescindible per evitar que unes característiques dominin sobre altres.
-
Avantatges: Simple, flexible, funciona bé amb fronteres no lineals.
-
Desavantatges: Lent en predicció, requereix molta memòria, maledicció de la dimensionalitat.
-
Comparació amb arbres de decisió: KNN és millor per datasets petits amb poques dimensions, mentre que arbres són millors per datasets grans amb moltes dimensions.
KNN és un algoritme fonamental en machine learning que, tot i la seva simplicitat, és sorprenentment efectiu en moltes aplicacions pràctiques. La seva comprensió ajuda a entendre conceptes importants com la importància de l’escalat de dades i els reptes de l’alta dimensionalitat.