Aprenentatge supervisat

• Introducció
  • Tipus d’aprenentatge supervisat
    • Regressió
    • Classificació
• Terminologia fonamental
  • Variables i dades
  • Model i predicció
  • Model lineal
• Funció de cost
  • Funció de cost d’error quadràtic
• Gradient Descent (Descens del Gradient)
  • Derivades i derivades parcials
  • Algorisme del Gradient Descent
  • Consideracions Importants
    • Actualització Simultània
    • Taxa d’Aprenentatge (α)
    • Convergència Natural
  • Mínims Locals vs Globals
  • Propietat Especial de la Regressió Lineal
• Descens del gradient alternatius
• Regressió Lineal Múltiple
  • Model de la Regressió Multiple
  • Codi Python
  • Gradient Descent per Múltiples Variables
• Escalat i normalització de característiques
  • Terminologia: escalat vs normalització
  • Mètodes de transformació
    • 1. Escalat mínim-màxim (Min-Max Scaling)
    • 2. Normalització per la mitjana (Mean Normalization)
    • 3. Estandardització z-score (Standardization)
  • Guia pràctica
• Convergència del Descens del Gradient
• Enginyeria de Característiques
• Regressió Polinòmica
• Regressió lineal amb Scikit-learn
• Classificació binària
  • Els 3 passos de la regressió logística
  • El model complet
  • Resum Visual
  • Conceptes Clau
  • Frontera de Decisió
  • Fronteres no lineals
  • Funció de cost
  • Taxa d’encerts (accuracy)
• Regressió logística amb Scikit-learn
• Sobreajustament i Subajustament
  • Regularització
    • Com funciona: Funció de cost amb regularització
    • Ajustar λ: el paràmetre clau
    • Descens del Gradient amb Regularització

Introducció

L’aprenentatge automàtic (Machine Learning) és una branca de la intel·ligència artificial que permet als algoritmes aprendre i millorar automàticament a partir de l’experiència, sense ser explícitament programats. Existeixen dos tipus principals d’aprenentatge: supervisat i no supervisat.

L’aprenentatge supervisat és un mètode on l’algoritme aprèn a partir de dades etiquetades, és a dir, se li proporcionen les respostes correctes durant l’entrenament.

Per contra, l’aprenentatge no supervisat treballa amb dades sense etiquetes, buscant patrons o estructures ocultes en les dades.

Característiques principals de l’aprenentatge supervisat:

• L’algoritme troba una línia o corba que representa la sortida donada l’entrada
• Utilitza dades d’entrenament amb exemples d’entrada i sortida coneguts
• L’objectiu és generalitzar per fer prediccions sobre dades noves

Tipus d’aprenentatge supervisat

Regressió

• Objectiu: Predir un número d’un conjunt infinit de possibles sortides
• Exemple: Predir el preu d’una casa basant-se en la seva mida
• Sortida: Valor numèric continu

Classificació

• Objectiu: Predir una categoria d’un conjunt finit de possibles valors (2 o més)
• Exemple: Determinar si un correu és spam o no
• Sortida: Classe o categoria discreta
• Funcionament: L’algoritme troba fronteres per separar les categories

Quan usar regressió vs classificació?

• Usa regressió quan la sortida és un valor continu (preu, temperatura, pes…)
• Usa classificació quan la sortida és una categoria discreta (spam/no spam, maligne/benigne…)

Terminologia fonamental

Variables i dades

• Dataset d’entrenament: Conjunt de dades utilitzat per entrenar el model
• x: Variable d’entrada o característica (feature)
• y: Variable de sortida o objectiu (target)
• (xᵢ, yᵢ): i-èssim exemple d’entrenament (una fila del dataset)
• m: Nombre d’exemples d’entrenament

Model i predicció

• f(x) = ŷ: Funció que representa el model i fa prediccions
• ŷ: Estimació o predicció del model (y amb accent circumflex)
• y: Valor real o objectiu

Model lineal

• f(x) = wx + b: Regressió lineal amb una variable
• w: Paràmetre de pes (weight) del model
• b: Paràmetre de biaix (bias) del model
• Els paràmetres w i b s’ajusten durant l’entrenament per millorar el model

Al següent gràfic es representa, a la coordenada x, una característica. I a la y, l’etiqueta. Com es tracta d’un model lineal, es representa com una línia.

Funció de cost

La funció de cost és una eina matemàtica fonamental que avalua globalment com de bé o malament s’ajusta el model al conjunt de dades. Es defineix habitualment com la mitjana de les funcions de pèrdua individuals, que mesuren l’error per a cada mostra. D’aquesta manera, la funció de cost assigna un valor numèric que representa l’“error total” del model: com més gran sigui aquest valor, pitjor és el rendiment, i com més petit sigui, millors són les seves prediccions.

Funció de cost d’error quadràtic

La funció de cost més utilitzada per a regressió lineal és l’error quadràtic:

J(w,b)=12mm∑i=1(f(xi)−yi)2

En paraules senzilles: Calculem l’error de cada predicció (diferència entre predicció i valor real), l’elevem al quadrat, i en fem la mitjana.

On:

• J(w, b): Funció de cost
• m: Nombre d’exemples d’entrenament
• f(xᵢ): Predicció per a l’exemple i
• yᵢ: Valor real per a l’exemple i

Per què aquesta fórmula?

• Divisió per m: Perquè l’error no depengui del nombre d’exemples d’entrenament
• Divisió per 2: Simplifica els càlculs futurs (especialment les derivades)
• Elevat al quadrat: Penalitza més els errors grans, evita que errors positius i negatius es cancel·lin, i fa la funció diferenciable a tot arreu

Objectiu d’Optimització: minimitzar J(w, b) per trobar els millors paràmetres del model.

Visualització:

• Si canviem només w: Obtenim una corba en forma de U
• Si canviem w i b: Obtenim una superfície 3D en forma de U
• El punt més baix representa els millors paràmetres

Aquesta és la representació quan tenim dues característiques:

Gradient Descent (Descens del Gradient)

És l’algoritme que troba els valors de w i b que minimitzen la funció de cost J(w, b).

Funcionament:

1. Inicialització: Comença amb w = 0 i b = 0
2. Iteració: Canvia w i b per reduir J(w, b)
3. Direcció: Fa passos en la direcció que més redueix la funció de cost
4. Convergència: S’atura quan arriba a un mínim local

Derivades i derivades parcials

Abans d’entendre l’algorisme matemàtic, necessitem comprendre què és una derivada.

Una derivada ens diu com de ràpid canvia una cosa.
Imagina que estàs en una muntanya russa. En cada moment:

• L’altura f(x) et diu on estàs. És la quantitat que canvia.
• La derivada de l’altura f′(x) et diu com de ràpid estàs pujant o baixant, és a dir, la pendent:
  • Si la derivada és positiva, estàs pujant.
  • Si és negativa, estàs baixant.
  • Si la derivada és 0, estàs en un punt pla (ni puges ni baixes).

La gràfica mostra:

• La corba és f(x)=x2
• La línea de punts és la tangent al punt seleccionat del slider
• La pendent de la línia és la derivada f′(x0)=2x0

I què és una derivada parcial respecte d’una variable? Vol dir que la funció depèn de més d’una variable. Per exemple:

f(x,y)=x2+y2

Aquí, la funció depèn de x i y.

La derivada parcial respecte de x és com canvia f si només canvies x, deixant y fix.
La derivada parcial respecte de y és com canvia f si només canvies y, deixant x fix.

🔍 És com mirar la pendent en una sola direcció, mentre les altres es mantenen iguals.

Algorisme del Gradient Descent

Ara que entenem què són les derivades, podem veure l’algorisme matemàtic:

w:=w−α×∂J∂wb:=b−α×∂J∂b

Què significa això?

• Calculem la derivada parcial (la pendent) de la funció de cost respecte a cada paràmetre
• Aquesta pendent ens diu en quina direcció augmenta l’error
• Restem un petit pas en aquesta direcció per reduir l’error
• α (alfa) controla la mida del pas que fem

En paraules senzilles: “Mira en quina direcció puja la muntanya (derivada) i fes un pas cap a l’altra banda (resta) per baixar.”

Consideracions Importants

Actualització Simultània

És crucial actualitzar w i b simultàniament en cada iteració per garantir el funcionament correcte de l’algoritme.

Taxa d’Aprenentatge (α)

• α massa petita: L’algoritme funcionarà però serà lent
• α massa gran: L’algoritme pot no convergir i “saltar” el mínim
• α adequada: Convergència eficient cap al mínim

Convergència Natural

A mesura que ens apropem al mínim, els passos es fan més petits automàticament perquè la derivada (pendent) disminueix.

Mínims Locals vs Globals

• Mínim local: El punt més baix d’una “vall” específica
• Mínim global: El punt més baix de tota la funció
• El punt d’inici pot determinar a quin mínim local arribem

Propietat Especial de la Regressió Lineal

La funció de cost d’error quadràtic amb regressió lineal té una propietat única: només té un mínim, que és el global. Això és perquè la funció de cost té forma de bol (funció convexa).

Per què importa la convexitat? Una funció convexa té la propietat que qualsevol mínim local és també un mínim global. Això garanteix que el descens del gradient sempre trobarà la millor solució possible, independentment del punt d’inici.

Descens del gradient alternatius

Batch (per lots complets) és la versió del gradient descent que utilitza tots els exemples d’entrenament en cada pas de l’algoritme. Aquesta és la versió que utilitzarem per a regressió lineal, tot i que existeixen alternatives que utilitzen subconjunts de dades per millorar el rendiment en datasets molt grans:

• Gradient Descent per mini-lots (Mini-Batch): actualitza els pesos usant un petit subconjunt de mostres, equilibrant velocitat i estabilitat.
• Gradient Descent estocàstic (SGD): actualitza els pesos usant una sola mostra a la vegada, introduint actualitzacions sorolloses però freqüents.

Regressió Lineal Múltiple

En regressió lineal múltiple utilitzem múltiples característiques (variables) per ajudar a predir.

Notació:

• Les característiques es numeren: x1,x2,x3,… Exemple: x1 = mida, x2 = habitacions, x3 = edat

• Per referir-nos a un exemple específic, posem un número entre parèntesis: →x(2) = totes les característiques de la casa número 2 x(2)3 = només l’edat de la casa número 2

Model de la Regressió Multiple

El nou model es defineix com:

f→w,b(→x)=→w⋅→x+b=w1x1+w2x2+⋯+wnxn+b

On:

• →w=[w1,w2,w3,…,wn] són els paràmetres del model
• →x=[x1,x2,x3,…,xn] són les característiques

I ⋅ representa el producte escalar (dot product), una operació entre dos vectors de la mateixa mida que retorna un escalar. L’operació es pot vectoritzar, que vol dir que es pot escriure sense bucles i executar-se amb una llibreria numèrica optimitzada per a matrius.

Codi Python

Sense vectorització:

import numpy as np

w = np.array([w1, w2, w3, ...])
b = 4
x = np.array([x1, x2, x3, ...])

f = 0
n = len(w)
for j in range(n):
    f += w[j] * x[j]
f += b

Amb vectorització:

import numpy as np

w = np.array([w1, w2, w3, ...])
b = 4
x = np.array([x1, x2, x3, ...])

f = np.dot(w, x) + b

Gradient Descent per Múltiples Variables

L’algorisme de descens del gradient s’actualitza per a cada paràmetre wj amb el següent pas:

wj:=wj−α∂J(→w,b)∂wjfor j=1…nb:=b−α∂J(→w,b)∂b

Escalat i normalització de característiques

Imagina que vols predir el preu d’una casa amb dues característiques:

• Mida: 50-300 m² (rang molt gran)
• Habitacions: 1-5 (rang petit)

El model tindrà dificultats perquè les escales són molt diferents.

Per què és un problema? Quan les característiques tenen rangs molt diferents, el descens del gradient es mou de forma ineficient, fent “zigzag” en lloc de baixar directament cap al mínim. Això fa que l’entrenament sigui molt més lent.

La solució: Transformar totes les característiques perquè tinguin escales similars. Això fa que el descens del gradient sigui molt més directe i ràpid.

Terminologia: escalat vs normalització

En aprenentatge automàtic, aquests termes s’utilitzen sovint de manera intercanviable, però tècnicament tenen significats diferents:

• Escalat (Scaling): Transformar les dades a un rang específic (per exemple, [0, 1] o [-1, 1])
• Normalització (Normalization): En sentit estricte, transformar les dades perquè tinguin propietats estadístiques específiques
• Estandardització (Standardization): Un tipus específic de transformació que centra les dades (mitjana = 0) i les escala per la desviació estàndard (std = 1)

En la pràctica, el terme “normalització” s’usa àmpliament per referir-se a qualsevol d’aquestes transformacions.

Mètodes de transformació

1. Escalat mínim-màxim (Min-Max Scaling)

Transforma les dades a un rang [0, 1]:

xesci=xi−min(x)max(x)−min(x)

Quan usar-lo: Quan necessites que totes les característiques estiguin en el mateix rang [0, 1]. Útil per algoritmes sensibles a la magnitud dels valors.

Desavantatge: Sensible a outliers (valors extrems).

2. Normalització per la mitjana (Mean Normalization)

Centra les dades al voltant de 0 i les escala pel rang:

xnormi=xi−μimax(x)−min(x)

On μi és la mitjana de la característica.

Quan usar-lo: Quan vols centrar les dades però mantenir un rang específic aproximadament entre -0.5 i 0.5.

3. Estandardització z-score (Standardization)

Transforma les dades per tenir mitjana 0 i desviació estàndard 1:

xstdi=xi−μiσi

On μi és la mitjana i σi és la desviació estàndard.

Quan usar-lo: El mètode més comú en ML. Menys sensible a outliers que Min-Max. És el que utilitza StandardScaler de scikit-learn.

Avantatge: No té límits definits (pot donar valors fora de [-1, 1] si hi ha outliers), però la majoria de valors queden típicament entre -3 i 3.

Guia pràctica

Els valors resultants solen quedar en rangs raonables. Si les teves característiques ja estan entre -0.3 i 0.3, o entre -3 i 3, potser no cal aplicar cap transformació.

Regla general: Usa estandardització Z-score per defecte, excepte quan necessitis específicament un rang [0, 1] (llavors usa Min-Max).

Convergència del Descens del Gradient

Per visualitzar la convergència, es representa la funció de cost J(w,b) al llarg de les iteracions. Aquesta és la corba d’aprenentatge, que sovint té forma de llei de potències.

• Si J augmenta, potser el pas α és massa gran.
• Després de moltes iteracions, J pot deixar de disminuir — això és la convergència.

Test automàtic de convergència: un criteri simple és definir un llindar de tolerància ε=0.001 (epsilon, un valor molt petit). Si el canvi de J entre iteracions és inferior a ε, considerem que ha convergit. Això és només un dels molts criteris possibles per determinar la convergència.

Elecció del Ritme d’Aprenentatge

• Massa gran: J augmenta o oscil·la per excés de pas.
• Massa petit: convergència molt lenta.

Una seqüència típica de valors per provar seria: α∈0.001,0.003,0.01,0.03,0.1,0.3

Per avaluar quin valor d’α funciona millor, podem utilitzar un conjunt de validació o tècniques com K-Fold Cross-Validation. Si cap funciona, cal revisar la implementació.

Enginyeria de Característiques

Fins ara hem utilitzat les característiques tal com ens les donaven. Però sovint podem millorar significativament el model creant noves característiques més informatives.

L’enginyeria de característiques consisteix a crear noves característiques a partir de les existents utilitzant el nostre coneixement del problema.

Exemple pràctic: Si volem predir el preu d’una casa i tenim:

• façana = 10 metres
• fons = 20 metres

Podem crear una nova característica més útil:

• superfície = façana × fons = 200 m²

Sovint, aquesta nova característica és més informativa que les originals per si soles. És com donar-li al model la informació ja “processada” de forma més útil.

Regressió Polinòmica

Què passa si les dades no segueixen una línia recta sinó una corba?

La regressió polinòmica ens permet ajustar corbes als nostres dades afegint termes com x2, x3, etc.

Exemple: y=w1x+w2x2+b

En lloc de només x (línia recta), també usem x2 (això crea una corba parabòlica).

Important: Quan afegim termes com x2 o x3, els valors poden créixer molt (per exemple, 1002=10000). Per això, l’escalat de característiques és essencial en regressió polinòmica.

També es poden fer altres transformacions com √x segons el problema.

Regressió lineal amb Scikit-learn

Implementarem amb scikit-learn un model per predir el preu d’una casa.

Assumim que el conjunt de dades es troba en un fitxer anomenat ‘houses.txt’ amb la primera fila com a capçalera i les característiques estan separades per comes. L’última columna és la variable objectiu (preus de les cases). El conjunt de dades s’ha d’estructurar de la següent manera: size(sqft),bedrooms,floors,age,price.

import numpy as np
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler

# Carregueu el conjunt de dades
data = np.loadtxt("./data/houses.txt", delimiter=",", skiprows=1)
X_train = data[:, :4]
y_train = data[:, 4]

X_features = ["size(sqft)", "bedrooms", "floors", "age"]

# Normalitzar les característiques
# Ús de StandardScaler per normalitzar les característiques

scaler = StandardScaler()
X_norm = scaler.fit_transform(X_train)
print(f"Peak to Peak range by column in Raw        X:{np.ptp(X_train,axis=0)}")
print(f"Peak to Peak range by column in Normalized X:{np.ptp(X_norm,axis=0)}")

# Entrena un model de regressió lineal utilitzant SGDRegressor

sgdr = SGDRegressor(max_iter=1000)
sgdr.fit(X_norm, y_train)
print(sgdr)
print(
    f"number of iterations completed: {sgdr.n_iter_}, number of weight updates: {sgdr.t_}"
)

# Mostrar els paràmetres del model

b_norm = sgdr.intercept_
w_norm = sgdr.coef_
print(f"model parameters:                   w: {w_norm}, b:{b_norm}")

# Feu prediccions sobre el conjunt d'entrenament

y_pred_sgd = sgdr.predict(X_norm)
y_pred = np.dot(X_norm, w_norm) + b_norm
print(
    f"prediction using np.dot() and sgdr.predict match: {(y_pred == y_pred_sgd).all()}"
)

print(f"Prediction on training set:\n{y_pred[:4]}")
print(f"Target values \n{y_train[:4]}")

El gràfic amb 4 subplots mostra cadascuna de les característiques respecte del preu real (punts blaus) i el preu predit (punts taronges). La línia vermella mostra la tendència real de cada estadística.

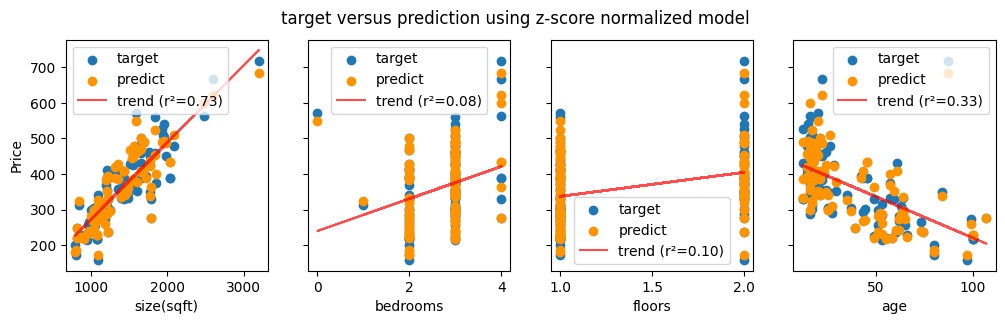
El que busquem és:

• Bon rendiment del model: els punts taronges haurien d’estar a prop dels punts blaus a cada gràfic.
• Relacions fortes: els valors de R² més alts signifiquen que la característica prediu fortament el preu: com de compactes s’agrupen les dades al voltant de la línia.
• Supòsits lineals: la línia de tendència vermella mostra si una relació lineal té sentit per a cada característica.

Per a les característiques discretes (dormitoris i pisos), es creen “columnes” verticals de punts perquè les cases només poden tenir nombres enters, cosa que fa que el format del diagrama de dispersió sigui menys intuïtiu.

Classificació binària

Imagina que vols separar dos tipus d’objectes diferents. La classificació binària funciona combinant les característiques dels teus exemples (les variables d’entrada) de manera similar a com ho fa la regressió lineal. El truc està en traçar una línia de separació (en 2D) o un pla de separació (en 3D) que divideix l’espai en dues regions: una per a cada classe. Aquest model s’anomena regressió logística.

Els 3 passos de la regressió logística

Per entendre com funciona realment la regressió logística, anem a desglossar el procés en 3 passos clars:

Pas 1: Calcular una puntuació (la combinació lineal):

Primer, calculem una puntuació per cada exemple combinant les seves característiques:

z=w⋅x+b

On:

• w són els pesos que ajustem durant l’entrenament
• x són les característiques d’entrada de l’exemple
• b és el terme independent (bias)
• z és la puntuació resultant

Exemple concret: Si volem predir si algú comprarà un producte segons la seva edat (30 anys) i ingressos (60.000€):

z=−5+0.1×30+0.00003×60.000=−0.2

Aquesta puntuació z pot ser qualsevol número (de -∞ a +∞). Però què significa? Encara no ho sabem… necessitem interpretar-la!

Pas 2: Interpretar la puntuació (el log odds):

Aquí ve la idea clau: aquesta puntuació z que acabem de calcular ja és el logaritme de les oportunitats (log odds) de pertànyer a una classe o l’altra!

Què vol dir això?

• Si z=0 → 50% de probabilitat per cada classe
• Si z>0 → més probable que sigui de la classe 1
• Si z<0 → més probable que sigui de la classe 0
• Com més gran el valor absolut de z, més segurs estem de la predicció

Pensa-ho com una línia numèrica:

Segur classe 0      Dubte      Segur classe 1
    -∞ <----------- 0 -----------> +∞

En el nostre exemple, z=−0.2 està una mica a l’esquerra del zero, així que l’exemple probablement pertany a la classe 0, però no estem molt segurs.

Pas 3: Convertir a probabilitat (la funció sigmoide):

Finalment, necessitem convertir aquesta puntuació z en una probabilitat que tothom pugui entendre (un número entre 0 i 1). Per això fem servir la funció sigmoide:

g(z)=11+e−zon0<g(z)<1

Per què és útil aquesta funció? Perquè agafa qualsevol número (sigui molt gran, molt petit, positiu o negatiu) i el “comprimeix” suaument a un valor entre 0 i 1.

La sigmoide té forma d’S i funciona així:

z = -10  →  g(z) ≈ 0.00005  (0%)    ← Gairebé segur classe 0
z = -2   →  g(z) ≈ 0.12     (12%)   
z = 0    →  g(z) = 0.5      (50%)   ← Punt central, dubte total
z = 2    →  g(z) ≈ 0.88     (88%)   
z = 10   →  g(z) ≈ 0.99995  (100%)  ← Gairebé segur classe 1

En el nostre exemple amb z=−0.2:

g(−0.2)≈0.45

Això vol dir que hi ha un 45% de probabilitat que l’exemple pertanyi a la classe 1, i per tant un 55% que sigui de la classe 0.

El model complet

Posant-ho tot junt, el nostre model de classificació binària és:

fw,b(x)=11+e−(w⋅x+b)=P(y=1∣x;w,b)

O dit d’una altra manera, més intuïtiva:

Característiques → [Puntuació z] → [Sigmoide] → [Probabilitat]
      x          →  w·x + b      →    g(z)    →    0 a 1

Aquesta expressió ens dona directament la probabilitat que l’entrada x pertanyi a la classe 1, donats els paràmetres w i b que hem après durant l’entrenament.

Resum Visual

• Puntuació negativa → probabilitat propera a 0 → quasi segur que és de la classe 0
• Puntuació positiva → probabilitat propera a 1 → quasi segur que és de la classe 1
• Puntuació propera a zero → probabilitat propera a 0.5 → incertesa total, podria ser de qualsevol classe

Conceptes Clau

Log Odds (Logit): El logaritme de les oportunitats. És el valor z que obtenim de la combinació lineal. Va de -∞ a +∞ i és simètric al voltant del zero.

Sigmoide: La funció matemàtica que converteix qualsevol número real en una probabilitat (valor entre 0 i 1). Té forma d’S i sempre passa pel punt (0, 0.5).

Regressió Logística: Un model de classificació que utilitza una combinació lineal de les característiques seguida d’una funció sigmoide per predir la probabilitat de pertànyer a una classe.

Frontera de Decisió

La frontera de decisió és la línia (o hiperpla en dimensions superiors) que separa les regions on el model prediu diferents classes.

Una regla comuna és:

ˆy={1,si g(z)>0.5,0,si no.

I com que g(z)>0.5 equival a z>0, es pot escriure directament:

ˆy=1⟺wTx+b≥0.

La frontera de decisió és el conjunt de tots els punts x per als quals el model està exactament al límit entre la classe 0 i la classe 1, és a dir, on

z=wTx+b=0.

Si x=(x1,x2) i w=(w1,w2), la frontera de decisió es descriu per
w1 x1+w2 x2+b=0.

Geomètricament, això és una línia al pla (x1,x2).

Tots els punts d’un costat (on w1x1+w2x2+b>0) es classifiquen com a 1, i els de l’altre costat com a 0.

Fronteres no lineals

Per obtenir corbes (cercles, el·lipses, etc.), podem ampliar el vector d’atributs amb termes polinòmics.

Si en lloc de (x1,x2) utilitzem (x21,x22) i aprenem pesos w1,w2 i biaix b, la frontera és
w1,x21+w2,x22+b=0.

Afegint pesos diferents o termes creuats es poden generar el·lipses rotades, paraboles o formes molt complexes, segons el grau i la combinació de termes polinòmics.

Funció de cost

Per a classificació, no podem usar l’error quadràtic (no funcionaria bé). En lloc d’això, s’utilitza la pèrdua logarítmica (entropia creuada):

L(fw,b(xi),yi)={−log(fw,b(xi))si yi=1−log(1−fw,b(xi))si yi=0

Per què aquesta funció? Penalitza molt les prediccions molt segures però incorrectes. Si el model està molt segur que és classe 1 (probabilitat alta) però en realitat és classe 0, el cost és enorme. Això força el model a aprendre millor.

Aquesta funció també garanteix que podem aplicar descens del gradient de forma eficient (és convexa).

Quan l’etiqueta real és 1 (corba verda):

• Si ˆy s’apropa a 1 → cost baix (la predicció és correcta i segura)
• Si ˆy s’apropa a 0 → cost molt alt (la predicció és completament errònia)

Quan l’etiqueta real és 0 (corba vermella):

• Si ˆy s’apropa a 0 → cost baix (predicció correcta)
• Si ˆy s’apropa a 1 → cost alt (predicció incorrecta)

Taxa d’encerts (accuracy)

Quan entrenem un model de classificació, necessitem una manera de saber fins a quin punt encerta les prediccions.
La taxa d’encerts (accuracy) és la mesura més senzilla i habitual.

Accuracy=Nombre de prediccions correctesNombre total de prediccions

En altres paraules, indica el percentatge de casos en què el model encerta la classe respecte al total de mostres.

Per exemple, si tenim 100 exemples i el model classifica correctament 90 d’ells, l’accuracy és:

90100=0.9(90%)

Limitació important: Datasets desbalancejats:

Un dataset desbalancejat és aquell on les classes no tenen una distribució similar. Per exemple:

• Detecció de frau: 99% transaccions normals, 1% fraudulentes
• Diagnòstic de malaltia rara: 98% pacients sans, 2% malalts

En aquests casos, l’accuracy pot ser molt enganyosa. Un model que sempre prediu “no frau” tindria 99% d’accuracy però seria completament inútil, ja que no detectaria cap frau real.

Per això, en problemes amb classes desbalancejades cal utilitzar mètriques més adequades com Precision, Recall i F1-Score, que avaluen millor la capacitat del model per detectar la classe minoritària.

Nota: Per a una anàlisi completa de com treballar amb datasets desbalancejats i les mètriques adequades, consulta la secció Classes Desbalancejades a la guia de mètriques d’avaluació.

Regressió logística amb Scikit-learn

import numpy as np
from sklearn.linear_model import LogisticRegression

X = np.array([[0.5, 1.5], [1,1], [1.5, 0.5], [3, 0.5], [2, 2], [1, 2.5]])
y = np.array([0, 0, 0, 1, 1, 1])

# Create and fit a logistic regression model
lr_model = LogisticRegression()
lr_model.fit(X, y)

# Predict on the training set
y_pred = lr_model.predict(X)

print("Prediction on training set:", y_pred)

# Calculate and print the accuracy on the training set
print("Accuracy on training set:", lr_model.score(X, y))

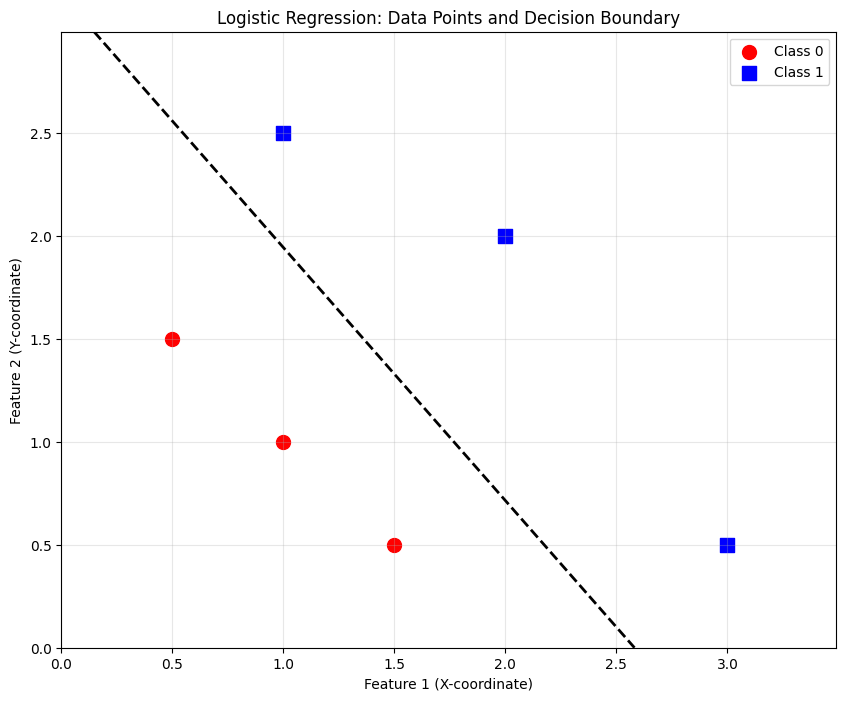
Sobreajustament i Subajustament

Hi ha dos problemes que poden produir-se quan estem entrenant el nostre model:

• Subajustament: model massa simple; alt biaix: el model no capta bé els patrons de les dades.
• Sobreajustament: massa complex; alta variància: model massa sensible a les dades.

Analogia: És com estudiar per un examen. El subajustament és quan no estudies prou i suspens. El sobreajustament és com memoritzar només les preguntes d’exàmens anteriors: encerts perfectament aquelles, però suspens amb preguntes noves perquè no has entès realment els conceptes.

Exemple concret: Imagina que entrenem un model amb un polinomi de grau 10 amb només 5 punts de dades. El model pot passar exactament per tots els punts d’entrenament (error zero!), però la corba serà extremadament tortuosa. Quan arriba una dada nova que no és exactament com les d’entrenament, la predicció serà completament errònia. El model ha “memoritzat” les dades en lloc d’aprendre el patró subjacent.

El sobreajustament implica alta precisió en entrenament però mala generalització.

Com evitar el sobreajustament:

1. Més dades d’entrenament.
2. Simplificar el model (menys característiques o polinomis més simples).
3. Regularització: penalitza pesos grans i redueix la complexitat.
   • Exemple: regularització L2 afegeix λ2m∑nj=1w2j a la funció de cost (tant per regressió com per classificació).

Regularització

La regularització és com posar límits de velocitat al model per evitar que vagi massa ràpid en qualsevol direcció.

Idea bàsica:

• Afegim una “penalització” quan els pesos w són massa grans
• Això força el model a ser més simple i suau
• Un model més simple generalitza millor a dades noves

Analogia: És com conduir amb limitadors de velocitat. Pots arribar al destí, però sense fer maniobres brusques que et facin sortir de la carretera (sobreajustament).

Què penalitzem?

• Penalitzem tots els pesos del model per igual
• Això evita que el model doni massa importància a una sola característica
• El resultat és un model més equilibrat i robust

Com funciona: Funció de cost amb regularització

Afegim un terme extra a la funció de cost:

J(w,b)=Error original+Penalització pels pesos grans

Matemàticament:

J(w,b)=Joriginal(w,b)+λ2mn∑j=1w2j

Components:

• λ (lambda): controla quanta penalització apliquem
• La suma ∑w2j: penalitza els pesos grans (els eleva al quadrat)
• Normalment no penalitzem b (el biaix)

Ajustar λ: el paràmetre clau

El valor de λ determina l’equilibri entre ajustar-se a les dades i mantenir el model simple:

• λ≈0: gairebé sense regularització → risc de sobreajustament
• λ moderat: equilibri òptim → bon ajust i bona generalització
• λ massa gran: model massa simple → pot donar sempre la mateixa predicció (subajustament)

L’objectiu amb regularització:

1. Minimitzar l’error en les dades d’entrenament
2. Mantenir els pesos petits per evitar complexitat excessiva

λ és qui controla aquest equilibri.

💡 Com escollim el millor λ? Podem usar un conjunt de validació per trobar el valor òptim de λ sense “fer trampes” amb les dades de test. Per obtenir una estimació més robusta, podem utilitzar K-Fold Cross-Validation.

Descens del Gradient amb Regularització

Amb regularització, l’actualització dels pesos té un terme addicional:

wj:=wj−α(Gradient normal+λmwj)

Què canvia?

• Mantenim el gradient normal (la direcció per reduir l’error)
• Afegim λmwj: un terme que “empeny” wj cap a zero

Efecte pràctic:

• Si un pes no ajuda gaire a reduir l’error, la regularització el farà més petit
• Els pesos només creixeran si realment milloren les prediccions
• Això evita que el model es compliqui innecessàriament

Nota: El biaix b normalment no es regularitza, només els pesos w.