Arbres de decisió

• Introducció
• Què és un arbre de decisió?
• Construcció d’un arbre
• Com escollir la millor pregunta?
  • Mesurar la barreja: l’entropia
  • Exemple: quina característica triem?
• Característiques contínues
• Hiperparàmetres: controlant la complexitat
  • Profunditat i sobreajustament
  • Validació creuada
  • Què fer si el model falla
• Conjunts d’arbres (ensembles)
  • Per què un sol arbre no és suficient?
  • Random Forest
  • Gradient boosting
• Quan usar arbres i quan xarxes neuronals?
• Més detalls
  • Criteri de Gini
  • Característiques amb més de dos valors
  • Arbres per a regressió
  • Importància de les característiques
  • Poda

Introducció

Farem servir un exemple senzill. Gestiones un centre d’adopció de gats i vols un classificador que, a partir d’unes quantes característiques d’un animal, decideixi ràpidament si és un gat o no.

Tens 10 exemples d’entrenament (5 gats i 5 gossos). Per a cada animal saps:

• Forma de les orelles (punxegudes o caigudes)
• Forma de la cara (rodona o no rodona)
• Bigotis (presents o absents)
• Etiqueta: és gat (1) o no és gat (0)

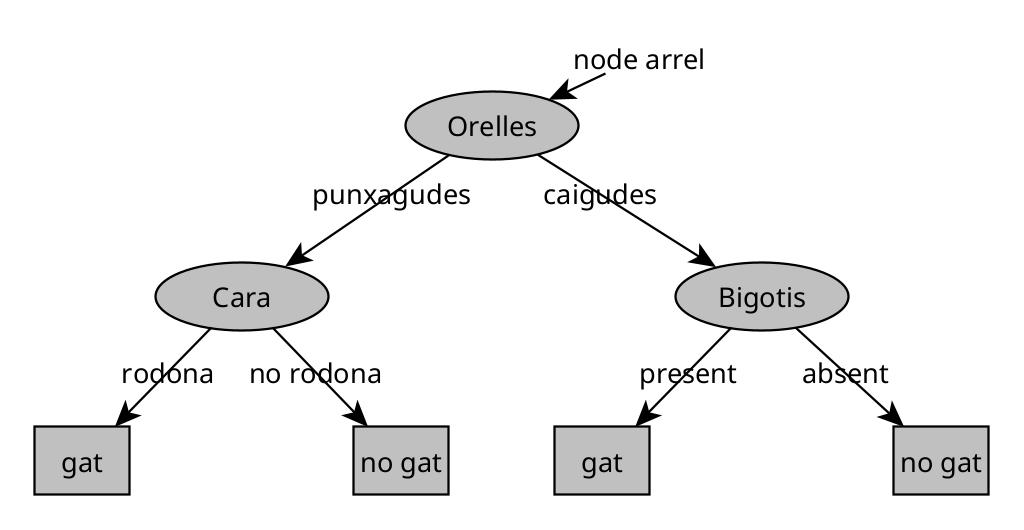
Per exemple, el primer animal té orelles punxegudes, cara rodona i bigotis, i és un gat. El segon té orelles caigudes, cara no rodona i bigotis, i també és un gat.

Com que l’etiqueta només pot ser 0 o 1, és un problema de classificació binària. De moment, cada característica només pren dos valors. Més endavant veurem què fer amb característiques contínues, com el pes.

Què és un arbre de decisió?

Un arbre de decisió és un model que, un cop entrenat, té forma d’arbre:

• Cada node de decisió (els ovals) fa una pregunta sobre una característica.
• El node arrel, a dalt de tot, és el punt de partida.
• Les fulles (les caixes de baix) donen la predicció final.

Per classificar un animal nou amb orelles punxegudes, cara rodona i bigotis:

1. Comencem a l’arrel, que pregunta: “Quina forma tenen les orelles?”
2. Segons la resposta, anem a l’esquerra o a la dreta.
3. El node següent potser pregunta: “La cara és rodona?”
4. Continuem baixant fins a una fulla, que diu: “És un gat”.

Les arrels a dalt i les fulles a baix semblen estranyes, però pensa-hi com en una planta penjant.

Amb les mateixes dades es poden construir molts arbres diferents: un que primer mira les orelles i després els bigotis, un altre que comença per la cara… L’algoritme d’aprenentatge ha de trobar un arbre que generalitzi bé, és a dir, que funcioni també amb animals que no ha vist.

Construcció d’un arbre

En aquest arbre s’hi ha afegit, entre parèntesis, quants animals arriben a cada node:

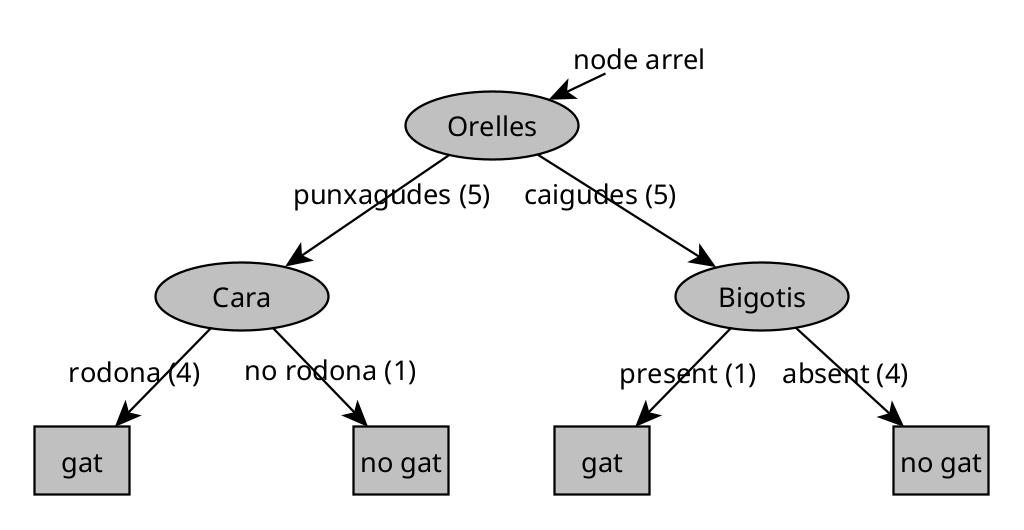
1. Arrel. Escollim la característica de l’arrel: la forma de les orelles. Els 5 animals amb orelles punxegudes van a l’esquerra, i els 5 amb orelles caigudes a la dreta.
2. Branca esquerra (4 gats i 1 gos). Dividim per la forma de la cara. Els 4 de cara rodona són tots gats: es converteix en una fulla “gat”. L’únic de cara no rodona és un gos: fulla “no gat”.
3. Branca dreta (1 gat i 4 gossos). Dividim pels bigotis. Amb bigotis queda el gat, sense bigotis els 4 gossos. Tots dos nodes són purs (només tenen una classe) i es converteixen en fulles.

Tot el procés es redueix a dues preguntes, que l’algoritme es fa a cada node:

1. Quina característica faig servir per dividir? La que deixa els grups més purs, amb menys barreja de gats i gossos.
2. Quan deixo de dividir? Quan el node ja és pur, quan s’arriba a una profunditat màxima, quan queden molt pocs exemples o quan la millora és massa petita.

L’algoritme és recursiu: aplica el mateix procés a cada branca.

funció construir_arbre(exemples):
    si cal parar (node pur, profunditat màxima, pocs exemples...):
        retorna fulla amb la classe majoritària

    característica = la que deixa els grups més purs
    dividir exemples segons característica

    retorna node(
        esquerra = construir_arbre(exemples_esquerra),
        dreta = construir_arbre(exemples_dreta)
    )

Com escollir la millor pregunta?

Imagina una bossa amb gats i gossos barrejats. Una bona pregunta és la que, en respondre-la, et deixa dues bosses on els animals s’assemblen més entre ells. L’ideal seria tots els gats a una banda i tots els gossos a l’altra.

Mesurar la barreja: l’entropia

Per mesurar com de barrejat està un grup fem servir l’entropia:

• Grup pur (tots gats o tots gossos): entropia 0
• Grup 50%-50%: entropia 1, la màxima confusió

El que importa és la intuïció: com més barrejat, més entropia.

Exemple: quina característica triem?

Tornem als 10 animals. Si provem les tres característiques:

“Orelles” deixa els grups més purs. Això es mesura amb el guany d’informació: quanta entropia eliminem amb la divisió.

• Orelles: 0.28, el guany més alt
• Bigotis: 0.12
• Cara: 0.03

Triem sempre la característica amb el guany més alt. El guany també ens diu quan parar: si és molt petit, dividir més només fa l’arbre més complex.

Característiques contínues

Què passa amb una característica contínua, com el pes de l’animal? De mitjana els gats pesen menys que els gossos, així que és una característica útil.

La pregunta ja no és “té orelles punxegudes?” sinó “pesa menys de X quilos?”, i l’algoritme ha de trobar el millor valor de tall.

El llindar pes ≤ 9 és el millor. Per trobar-lo, l’algoritme ordena els exemples per pes, prova cada punt mitjà entre dos exemples consecutius i es queda amb el que dona més guany. Amb 10 exemples, prova 9 llindars.

Hiperparàmetres: controlant la complexitat

Els hiperparàmetres són els “botons” que fixem abans d’entrenar i que decideixen com de complex serà l’arbre:

Profunditat i sobreajustament

Un arbre sense límit de profunditat pot créixer fins que cada fulla tingui un sol exemple. Tindrà un 100% d’encerts amb les dades d’entrenament, perquè les ha memoritzat, i fallarà amb dades noves.

És el mateix biaix i variància que vam veure amb els polinomis: el grau del polinomi ara és la profunditat de l’arbre.

Validació creuada

Per triar la profunditat provem diversos valors i mirem quin dona millors resultats amb dades de validació. Però amb una sola divisió el resultat depèn de la sort: de quins exemples han caigut a cada banda.

La validació creuada (cross-validation) ho resol. Dividim les dades d’entrenament en K parts (típicament 5), entrenem K vegades deixant cada vegada una part diferent per validar, i fem la mitjana dels K resultats. Cada exemple serveix tant per entrenar com per validar, i el resultat és més estable. Ho expliquem amb un gràfic a Validació creuada.

GridSearchCV prova totes les combinacions d’hiperparàmetres amb validació creuada i es queda amb la millor. Ho provem amb el dataset breast_cancer de scikit-learn: 30 mesures de 569 tumors, i com a objectiu si el tumor és maligne.

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.tree import DecisionTreeClassifier

data = load_breast_cancer()
X, y = data.data, 1 - data.target  # 1 = maligne
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, stratify=y, random_state=42)

# Valors a provar
param_grid = {
    'max_depth': [3, 5, 10, 20, None],
    'min_samples_split': [2, 5, 10],
    'min_samples_leaf': [1, 2, 4]
}

# cv=5: validació creuada amb 5 parts
tree = DecisionTreeClassifier(random_state=42)
search = GridSearchCV(tree, param_grid, cv=5, scoring='accuracy')
search.fit(X_train, y_train)

print(f"Millors paràmetres: {search.best_params_}")
print(f"Millor resultat: {search.best_score_:.3f}")

# El test només es mira al final, amb el model ja triat
print(f"Test: {search.score(X_test, y_test):.3f}")

Millors paràmetres: {'max_depth': 10, 'min_samples_leaf': 1, 'min_samples_split': 5}
Millor resultat: 0.938
Test: 0.939

La validació creuada estimava un 93.8% d’encerts i el test en dona un 93.9%: l’estimació era fiable. GridSearchCV ha provat 45 combinacions (5 × 3 × 3), cadascuna 5 vegades, i al final reentrena el model guanyador amb tot el conjunt d’entrenament.

Consells pràctics:

• Comença simple: max_depth=5 és un bon punt de partida.
• Compara entrenament i validació: si l’entrenament és molt millor, l’arbre és massa complex.
• Amb pocs exemples, limita més la profunditat.

Què fer si el model falla

Amb l’error d’entrenament i el de validació ja podem decidir què provar:

La taula completa de remeis, vàlida per a qualsevol model, és a Què fer si el model falla.

Conjunts d’arbres (ensembles)

Un ensemble fa treballar molts models junts. En lloc de confiar en un sol arbre, entrenem molts arbres i combinem les seves prediccions.

Per què un sol arbre no és suficient?

Un arbre és molt sensible a petits canvis en les dades: si canviem un sol exemple, la característica de l’arrel pot canviar i l’arbre resultant pot ser totalment diferent. Combinant molts arbres, cap d’ells té massa influència.

La combinació més senzilla és una votació:

Resultat: 2 vots a 1, guanya gat.

Random Forest

Si entrenem tots els arbres amb les mateixes dades, sortiran idèntics. El Random Forest fa que cada arbre sigui diferent amb dues tècniques:

1. Mostreig amb reposició (bagging): cada arbre s’entrena amb una mostra diferent de les dades. Traiem exemples a l’atzar i els tornem a posar a la bossa, de manera que uns es repeteixen i d’altres no hi apareixen.

   Dades originals	Mostra 1	Mostra 2	Mostra 3
   A, B, C, D, E	A, A, C, D, E	B, C, C, D, E	A, B, D, D, E

2. Característiques a l’atzar: a cada node, l’arbre només pot triar entre un subconjunt aleatori de les característiques. Això el força a explorar camins diferents.

Per predir, cada arbre vota i guanya la majoria.

from sklearn.ensemble import RandomForestClassifier

rf = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=42)
rf.fit(X_train, y_train)
print(f"Test: {rf.score(X_test, y_test):.3f}")

Gradient boosting

El gradient boosting segueix una estratègia diferent: en lloc d’arbres independents que voten, construeix els arbres un darrere l’altre, i cada arbre nou s’entrena per corregir l’error que encara cometen els anteriors. La predicció final és la suma de tots.

És com la pràctica deliberada al piano: en lloc de tocar la peça sencera una vegada i una altra, et concentres en els compassos que encara no et surten.

Les implementacions més utilitzades són XGBoost, LightGBM i, dins de scikit-learn, HistGradientBoostingClassifier.

from sklearn.ensemble import HistGradientBoostingClassifier

gb = HistGradientBoostingClassifier(max_iter=200, random_state=42)
gb.fit(X_train, y_train)
print(f"Test: {gb.score(X_test, y_test):.3f}")

# Alternativa: from xgboost import XGBClassifier
# Per a regressió: HistGradientBoostingRegressor o XGBRegressor

Amb les dades de tumors, el millor arbre sol que ha trobat GridSearchCV encerta el 93.9% del test. El Random Forest i el gradient boosting arriben al 97.4%, sense ajustar res: és la millora típica d’un ensemble sobre un arbre sol.

Amb dades en forma de taula, el gradient boosting continua sent l’opció per defecte en molts problemes reals, tot i que no sempre és el guanyador.

Quan usar arbres i quan xarxes neuronals?

• Dades en taules (preus, clients, transaccions): comença amb gradient boosting.
• Imatges, vídeo, àudio, text: fes servir xarxes neuronals, normalment a partir d’un model preentrenat.
• Si dubtes amb dades tabulars, prova tots dos i compara’ls amb validació.

Més detalls

Criteri de Gini

El criteri de Gini (o impuresa de Gini) és una alternativa a l’entropia per mesurar la barreja. La intuïció: si agafes dos animals a l’atzar del grup, quina probabilitat hi ha que siguin de classes diferents?

Totes dues valen 0 quan el grup és pur i són màximes quan està més barrejat, i a la pràctica donen resultats molt semblants. scikit-learn fa servir Gini per defecte perquè és una mica més ràpid de calcular (no necessita logaritmes):

from sklearn.tree import DecisionTreeClassifier

model = DecisionTreeClassifier(max_depth=3, random_state=42)  # Gini per defecte
# model = DecisionTreeClassifier(max_depth=3, criterion='entropy')
model.fit(X_train, y_train)

Característiques amb més de dos valors

Si les orelles poden ser punxegudes, caigudes o ovalades, creem una columna per a cada valor:

Això s’anomena codificació one-hot, perquè a cada fila només una columna està “encesa”. També la necessiten els models que fan operacions matemàtiques amb les dades (regressió, xarxes neuronals), perquè no es pot multiplicar “punxegudes” per un pes.

import pandas as pd

df = pd.DataFrame({'orelles': ['punxegudes', 'ovalades', 'caigudes']})
encoded = pd.get_dummies(df, columns=['orelles'])
print(encoded)
#    orelles_caigudes  orelles_ovalades  orelles_punxegudes
# 0             False             False                True
# 1             False              True               False
# 2              True             False               False

Arbres per a regressió

Els arbres també poden predir números, com el pes d’un animal. La mecànica és la mateixa amb dos canvis:

Si una fulla conté animals de 7.2, 7.6, 10.2 i 8.4 kg, la predicció és la mitjana: 8.35 kg. Un bon tall agrupa animals amb pesos semblants (7, 8 i 9 kg), on la mitjana és representativa, i evita grups dispersos (5, 12 i 20 kg), on la mitjana no representa ningú.

Importància de les característiques

Un arbre ens diu quines característiques li han estat més útils. La importància (feature importance) mesura quanta barreja elimina cada característica a tot l’arbre. Una característica que s’usa a prop de l’arrel afecta molts exemples i és molt important. Una que no s’usa mai té importància 0.

Serveix per entendre què mira el model, per explicar-ne les decisions i per detectar problemes: si una característica inesperada és molt important, potser hi ha un error a les dades.

import pandas as pd
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt

importances = pd.DataFrame({
    'característica': data.feature_names,
    'importància': model.feature_importances_
}).sort_values('importància', ascending=False)
print(importances)

# Dibuixar l'arbre (només és llegible amb arbres petits, max_depth <= 5)
plt.figure(figsize=(15, 8))
plot_tree(model, feature_names=data.feature_names, class_names=['benigne', 'maligne'], filled=True, rounded=True)
plt.show()

Poda

Una alternativa als hiperparàmetres és la poda posterior (post-pruning): deixar créixer l’arbre sencer i després tallar les branques que no aporten. A la pràctica, limitar la complexitat amb hiperparàmetres és més habitual i sol ser suficient. scikit-learn ofereix la poda amb el paràmetre ccp_alpha.