Recursivitat
- Conceptes
- Implementació
- Model d’execució
- Verificació dels mètodes recursius
- Altres activitats
- Activitats gràfiques
Conceptes

La recursivitat permet resoldre problemes en dos passos:
- Fent versions més petites del problema, repetidament, fins que tenim una mida de solució senzilla (obrim les nines).
- Combinant les solucions i s’obté la solució al problema inicial (les tornem a tancar)
La recursivitat és una eina poderosa, però pot ser menys eficient que solucions iteratives del mateix problema. Però a vegades és més senzill.
RECURSIVITAT = tipus de DESCOMPOSICIÓ de problemes
Exemple de recursivitat: factorial
En matemàtiques, el factorial n! és el número de permutacions de n elements:
n! = n * (n - 1) * (n - 2) * … * 2 * 1
Però també es por definir recursivament:
n! = 1, si n = 0 (cas base)
n! = n * (n - 1)! si n > 0 (cas general)
Per exemple:
1) 4! = 4 * 3!
2) 3! = 3 * 2!
3) 2! = 2 * 1!
4) 1! = 1 * 0!
5) 0! = 1 (cas base)
6) 1! = 1 * 0! = 1 * 1 = 1
7) 2! = 2 * 1! = 2 * 1 = 2
8) 3! = 3 * 2! = 3 * 2 = 6
9) 4! = 4 * 3! = 4 * 6 = 24
Implementació
A l’hora de decidir-se per una versió recursiva respecte d’una iterativa:
- S’ha de considerar si la solució recursiva és clara i eficient
- L’eficiència es pot mesurar en temps i espai (memòria)
- Algunes solucions són per definició ineficients
- Veure l’ordre de complexitat de l’algorisme recursiu i comparar-lo amb la seva versió iterativa
Activitat: factorial
Pensa com es podria implementar la funció factorial.
A Java, un mètode pot invocar un altre, fins i tot a si mateix!
Implementació del factorial:
public static int factorial(int n) {
if (n == 0) { // cas base
return 1;
}
else { // cas general
return n * factorial(n - 1);
}
}
Pregunta: què passaria si no hi hagués un cas base?
Activitat: canvi de base
Donat un número decimal, mostrar el seu valor binari.
Pista: divideix el número per 2 consecutivament per calcular cada xifra binària.
- Explica com es pot calcular a mà
- Pensa en un algorisme iteratiu
- Pensa com es podria convertir en recursiu
- Codifica l’algorisme
Activitat: potència
Donats dos nombres sencers b (base) i n (exponent), calcula b elevat a n, tenint en compte que b elevat a 0 = 1.
Fes-te les següents preguntes:
- Defineix el mètode que farà el càlcul: valor de retorn i paràmetres
- Com es pot calcular iterativament?
- Quants paràmetres tindrà el mètode que realitzi en càlcul?
Per fer la versió recursiva, pensa en els possibles valors de n per trobar
- el cas base: per quina n podem acabar la recursió?
- el cas general: com calcular la potència per un cas més petit?
Model d’execució
processador (CPU) ⇒ comptador de programa (PC)
molles de pa ⇒ permet tornar enrere al lloc on es va produir la crida ⇒ STACK
A la memòria tenim: codi i dades.
A les dades, hi ha dos espais de memòria importants:
- el heap: és un espai on viuen els objectes i on es fa el garbage collection
- el stack: és una pila (LIFO) on viuen les invocacions de mètodes d’un fil (thread). L’últim és el mètode que s’executa actualment.
Quan s’invoca un mètode s’afegeix un element (stack frame) al stack que conté:
- Els paràmetres
- Les variables locals creades
- L’adreça de retorn del mètode (cap, per al primer stack frame)
Quan es crea un objecte s’afegeix al heap, i es crea una referència a ell. Aquest espai es pot recuperar quan no hi ha més referències (garbage collection).
Exemple: quadrat
Al següent codi es calcula el quadrat d’un número.

Aquest seria el contingut dels stack frames a la línia 20 (PC = 20), si l’argument és “5” (stack frame):
| Paràmetres | Retorn | Variables locals |
|---|---|---|
| num = 5 | 15 | calc = 25 |
| args = { “5” } | (exit) | n = 5, nal2 = ? |
Exemple: hipotenusa
Al següent codi es fa el càlcul de la hipotenusa. Imaginem que tenim tres stack frames:
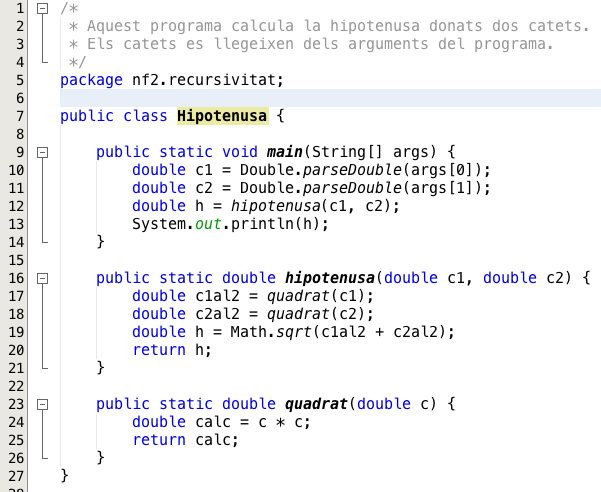
Com seria el contingut dels stack frames si el PC és 25, s’està calculant c1al2 i els arguments “3” i “5”?
Verificació dels mètodes recursius
Per veure si una solució recursiva funciona, la resposta ha de ser “sí” a aquestes tres preguntes:
- (Cas base) Hi ha una forma no recursiva de sortir del mètode, i el mètode funciona bé per aquest cas?
- (Cas més petit): Cada crida recursiva al mètode, involucra un cas més petit del problema original, que finalment arribarà al cas base?
- (Cas general): Si les crides recursives funcionen, funcionarà també el mètode?
Activitat. Per al factorial:
- Sí, el cas base passa si n = 0, i es retorna 1 sense més crides recursives.
- Sí, el cas més petit és factorial(n - 1), que finalment arribarà a factorial(0).
- Sí, el cas general és n * factorial(n-1), i si la crida recursiva funciona per n - 1 llavors ha de funcionar per a la fórmula.
Execució del factorial
Aquest seria el codi de l’execució del factorial:
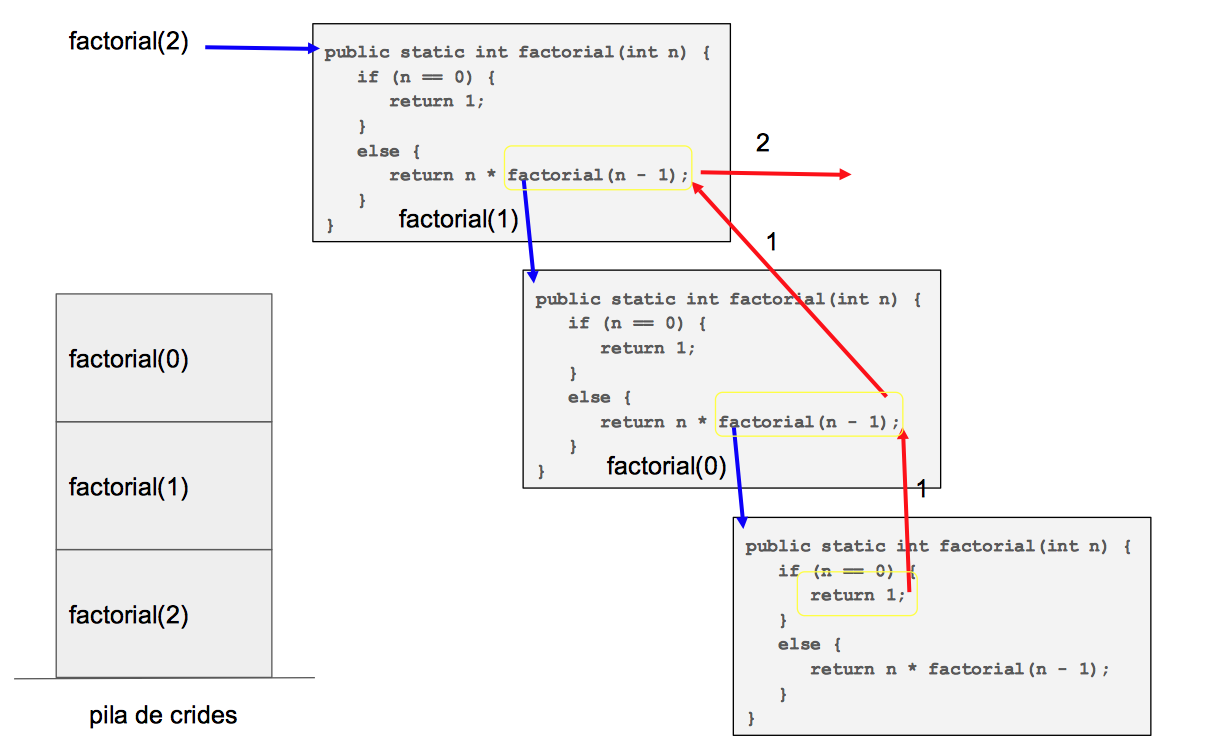
Aquests serien els stack frames:

Activitat: depuració de mètodes recursius
- Depura amb el teu IDE el mètode factorial
- Afegeix un breakpoint al començament del mètode
- Comprova el valor de n i el flux de control en funció del seu valor
- Mira la finestra de depuració i comprova el call stack
- Per cada call stack, mira el valor de n
Execució de la conversió a binari
Conversió a binari de 13 (1101):

Altres activitats
Aquestes són altres possibles activitats:
- Si un número és parell o senar (recursivitat creuada o indirecta)
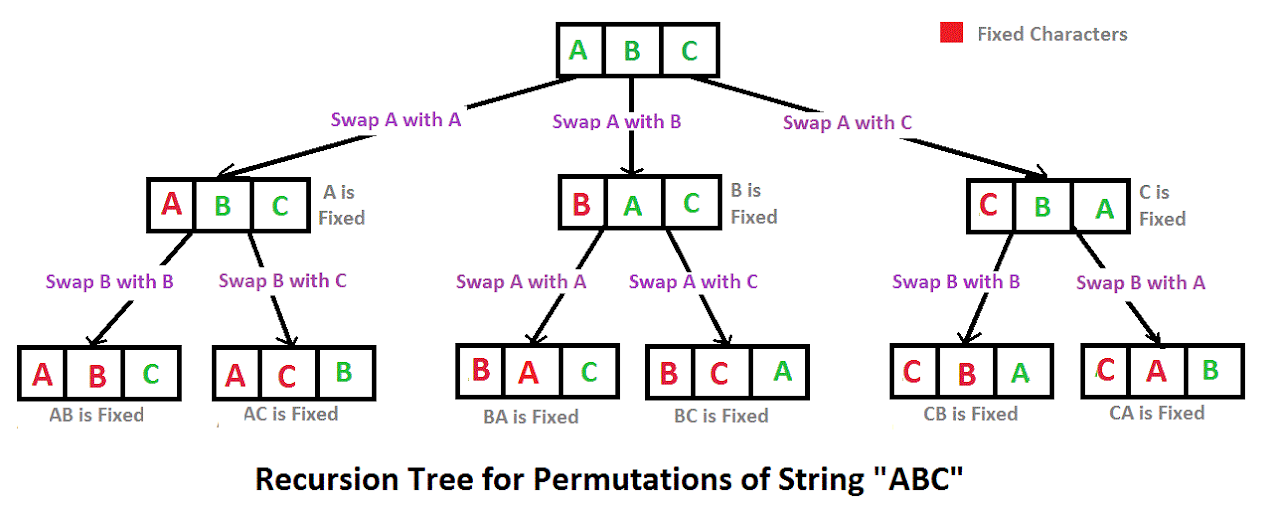
- Mostrar les permutacions per N lletres (veure imatge)
- Els números de Fibonacci (recursivitat múltiple)
- Els números d’Ackermann (recursivitat niada)
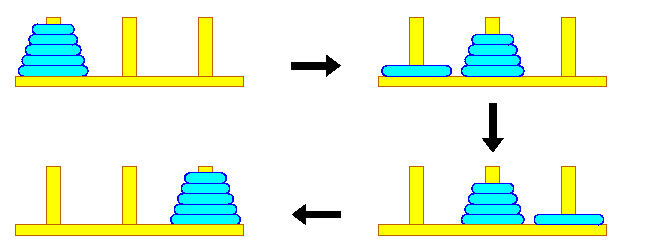
- Les torres d’Hanoi
Els nombres de Fibonacci són una successió matemàtica de nombres naturals tal que cada un dels seus termes és igual a la suma dels dos anteriors. Suposa F(0) = 0 i F(1) = 1,
Els nombres d’Ackermann és una funció recursiva amb dos nombres naturals com arguments que retorna un altre natural. Si la funció és A(m, n), el resultat és:
- n+1, si m = 0
- A(m-1, 1), si m > 0 i n = 0
- A(m-1, A(m, n-1)), si m > 0 i n > 0
Les torres d’Hanoi consisteixen en tres varetes verticals i un nombre indeterminat de discs de mides diferents que determinen la complexitat de la solució.
A l’inici estan col·locats de més gran a més petit en la primera vareta.
El joc consisteix a passar tots els discs a la tercera vareta tenint en compte que només es pot canviar de vareta un disc cada vegada i que mai no podem tenir un disc col·locat sobre un que sigui més petit.
Activitats gràfiques
Per a aquesta secció, pots utilitzar una llibreria gràfica de java basada en AWT o similar. Per exemple, StdDraw.
StdDaw:
- És una classe amb mètodes estàtics
- Per defecte, crea un espai amb coordenades (0,0) a (1,1)
- Copieu l’arxiu StdDraw.java al vostre projecte i proveu això:
Per exemple, la pots provar amb:
public class TestStdDraw {
public static void main(String[] args) {
StdDraw.setPenRadius(0.05);
StdDraw.setPenColor(StdDraw.BLUE);
StdDraw.point(0.5, 0.5);
StdDraw.setPenColor(StdDraw.MAGENTA);
StdDraw.line(0.2, 0.2, 0.8, 0.2);
}
}
Addicionalment, pots utilitzar una abstracció molt comuna, la tortuga. Aquesta és una possible definició del contracte que hauries d’implementar:
public interface Turtle {
void up(); // Sets the turtle up (not drawing)
void down(); // Sets the turtle down (drawing)
void left(double delta); // Turn delta degrees to the left
void right(double delta); // Turn delta degrees to the right
void forward(double step); // Go forward (drawing if it's down)
void backward(double step); // Go backward (drawing if it's down).
}
Un exercici interessant és dibuixar polígons estrella.
L’angle en graus per dibuixar els polígons d’aquestes estrelles es pot calcular com:
angle = 180 - (180 * p - 360 * q) / p
on p és el nombre de vertex i q el nombre de voltes.
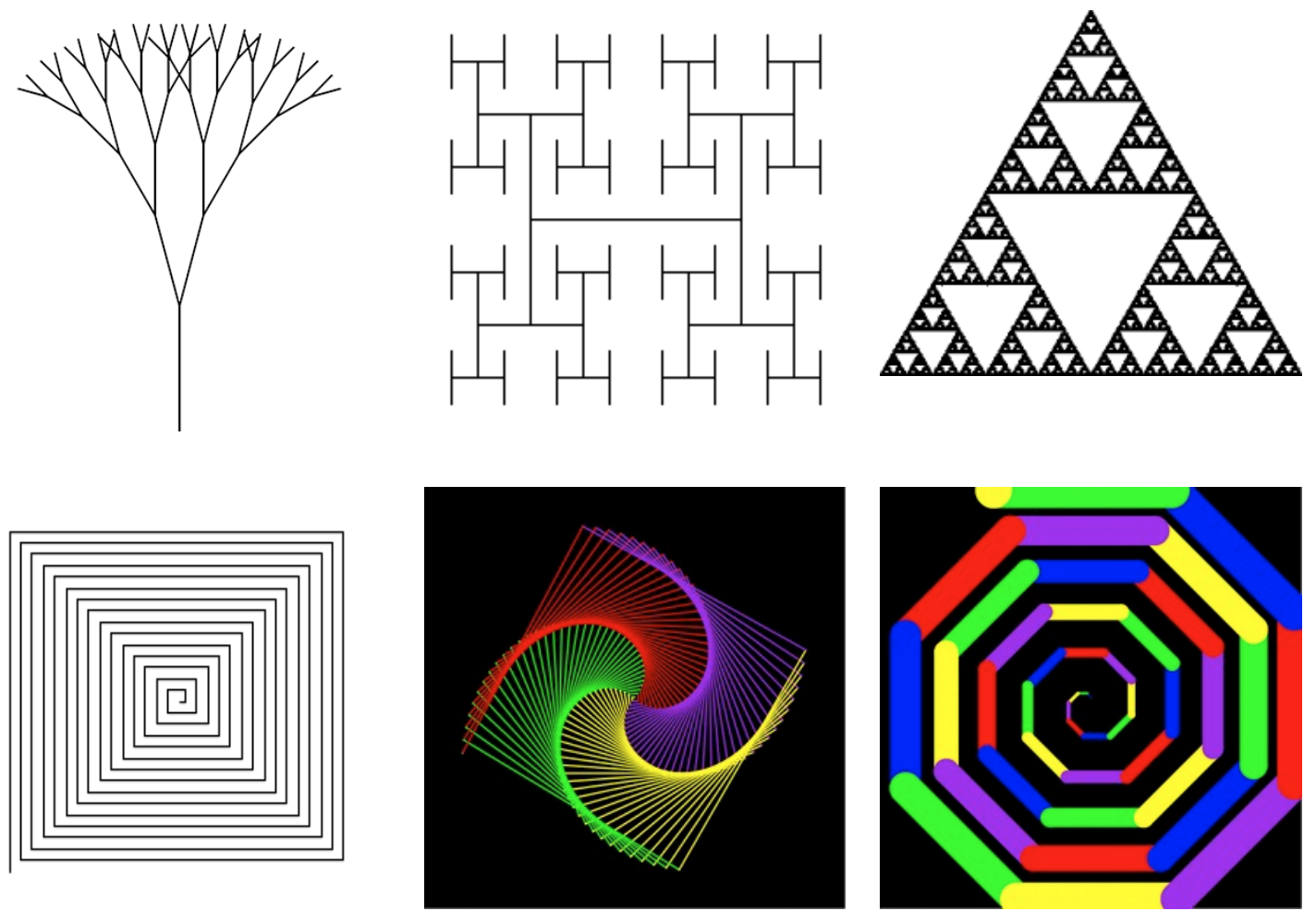
Dibuixeu les següents figures recursives:
- Espiral
- Arbre recursiu
- Htree
- Triangle Sierpinski
- Espiral amb els costats de colors
- Espiral amb vuit costats
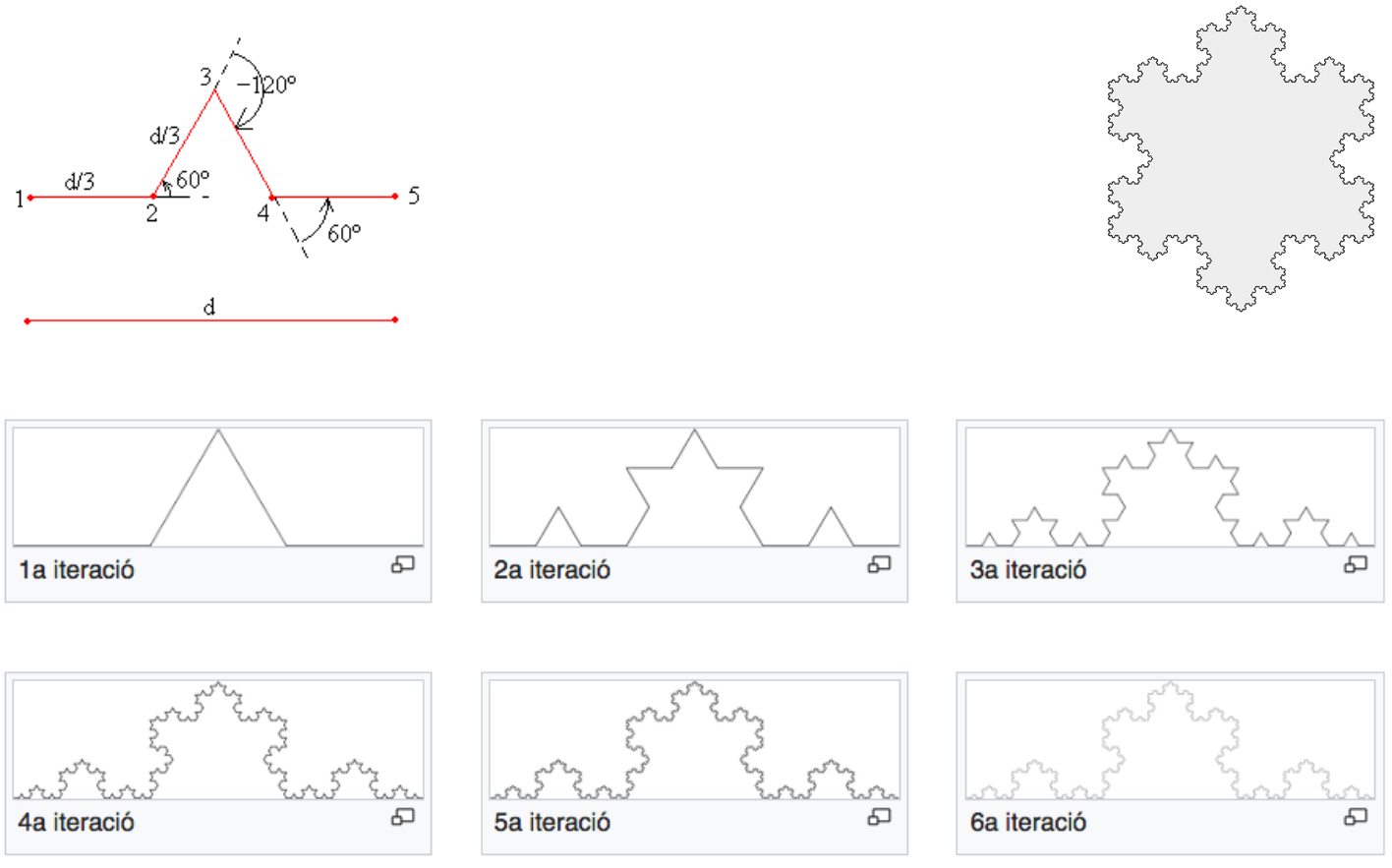
- Floc de neu de Koch