Arbres de decisió
- Introducció
- Què és un arbre de decisió?
- Diversos arbres possibles
- Construcció d’un arbre de decisió
- Com escollir la millor pregunta?
- Algorisme de l’arbre de decisió
- Codificació One-Hot
- Característiques contínues
- Arbres de decisió per a regressió
- Hiperparàmetres: controlant la complexitat
- Importància de les característiques
- Conjunts d’arbres (Ensembles)
- Quan usar arbres vs xarxes neuronals?
Introducció
Per entendre com funcionen els arbres de decisió, farem servir un exemple senzill:
Suposeu que gestioneu un centre d’adopció de gats i que, donades algunes característiques d’un animal, voleu entrenar un classificador que decideixi ràpidament si es tracta d’un gat o no.
Disposem de 10 exemples d’entrenament. Per a cada animal tenim les característiques següents:
- Forma de les orelles (punxegudes o caigudes)
- Forma de la cara (rodona o no rodona)
- Bigotis (present o absent)
- Etiqueta: és gat (1) o no és gat (0)
Exemple:
- El primer animal té orelles punxegudes, cara rodona, bigotis presents → és un gat.
- El segon té orelles caigudes, cara no rodona, bigotis presents → també és un gat.
- I així successivament fins a completar els 10 exemples (5 gats i 5 gossos).
Formalment:
- Les entrades X són les tres columnes de característiques.
- La sortida Y és la columna final que indica si és gat o no.
Com que Y∈0,1, es tracta d’un problema de classificació binària.
En aquest exemple, cada característica X1,X2,X3 només pot prendre dos valors possibles (categòrics). Més endavant veurem com treballar amb característiques multivaluades o fins i tot contínues.
Què és un arbre de decisió?
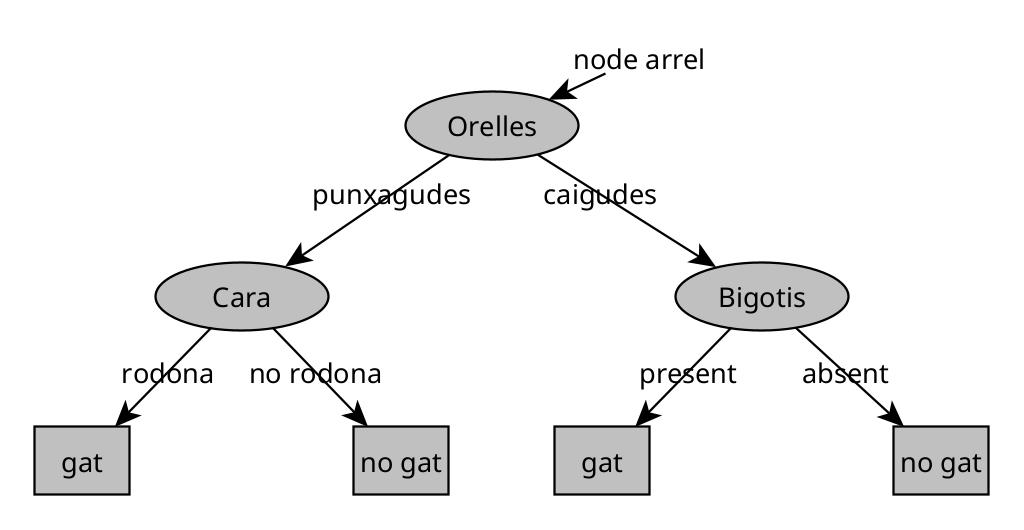
Un arbre de decisió és un model que, després d’entrenar-se amb dades, pren la forma d’una estructura jeràrquica anomenada arbre.
- Cada oval dins l’arbre és un node de decisió.
- El node arrel (a dalt de tot) és el punt de partida per classificar qualsevol exemple.
- Les fulles (caixes rectangulars a baix) representen les prediccions finals.
Funcionament
Si entra un nou exemple (p. ex., animal amb orelles punxegudes, cara rodona i bigotis presents), el procés és:
- Comencem al node arrel, que pot preguntar: “Quina és la forma de les orelles?”.
- Segons la resposta (punxegudes/caigudes), anem cap a l’esquerra o cap a la dreta.
- Al següent node, potser es pregunta: “La cara és rodona?”.
- Continuem baixant per l’arbre fins arribar a una fulla, que dona la predicció: “És un gat”.
👉 Encara que sembli estrany que les “arrels” siguin a dalt i les “fulles” a baix, penseu-ho com una planta penjant d’interior.
Diversos arbres possibles
Un mateix conjunt de dades pot donar lloc a molts arbres diferents.
Per exemple, podem tenir:
- Un arbre que primer mira les orelles i després els bigotis.
- Un altre que primer mira la cara i després les orelles.
- Altres variants amb criteris diferents.
Cadascun d’aquests arbres pot tenir un rendiment millor o pitjor sobre el conjunt d’entrenament, validació o test. La tasca de l’algoritme d’aprenentatge és trobar, entre tots els arbres possibles, un que generalitzi bé: és a dir, que tingui bon rendiment no només amb les dades vistes, sinó també amb noves dades.
Resumint:
- Els arbres de decisió permeten classificar exemples a partir d’un procés seqüencial de preguntes sobre les característiques.
- Cada node representa una decisió basada en una característica.
- Cada fulla representa una predicció final.
- Podem construir molts arbres diferents amb el mateix conjunt de dades; el repte és trobar-ne un que funcioni bé en general.
Construcció d’un arbre de decisió
El procés de construir un arbre de decisió a partir d’un conjunt d’entrenament es pot entendre en diversos passos. Vegem-ne el funcionament amb un exemple senzill de 10 mostres de gats i gossos.
En el següent arbre s’ha afegit el nombre d’animals que coincideixen amb el criteri de decisió (entre parèntesis):
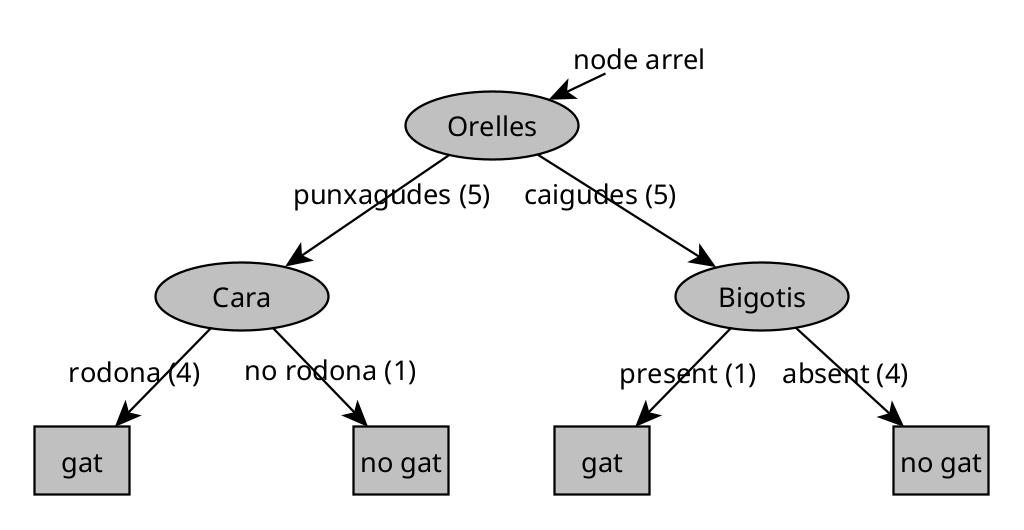
Pas 1. Escollir la característica de l’arrel
El primer pas és decidir quina característica utilitzarem al node arrel (el node superior de l’arbre).
Mitjançant un algoritme (que veurem més endavant), suposem que escollim la forma de les orelles.
- Els 5 exemples amb orelles punxegudes van al subarbre esquerre.
- Els 5 exemples amb orelles caigudes van al subarbre dret.
Pas 2. Dividir el subarbre esquerre
Ara ens fixem només en les 5 mostres amb orelles punxegudes. Hem de decidir una nova característica per dividir.
Imaginem que escollim la forma de la cara.
- 4 mostres tenen cara rodona → baixen a l’esquerra.
- 1 mostra té cara no rodona → baixa a la dreta.
Com que les 4 mostres amb cara rodona són totes gats, aquest node es converteix en un node fulla que preveu “gat”.
El node de la dreta conté un gos (100%), així que també es crea un node fulla que preveu “no gat”.
Pas 3. Dividir el subarbre dret
Passem al subarbre dret (les 5 mostres amb orelles caigudes). Aquí hi ha 1 gat i 4 gossos.
Suposem que escollim la característica bigotis.
- Si hi ha bigotis → queda 1 gat (100%).
- Si no hi ha bigotis → queden 4 gossos (100%).
Tots dos nodes són purs (conté només una classe), de manera que es converteixen en fulles: “gat” i “no gat”.
Decisions clau en l’aprenentatge d’arbres de decisió
Durant el procés hem de prendre diverses decisions importants:
1. Quina característica escollir en cada node?
En cada node amb una barreja de gats i gossos, l’algoritme ha de decidir quina característica és millor per dividir:
- forma de les orelles,
- forma de la cara,
- bigotis, etc.
La idea és maximitzar la puresa de les divisions.
Per exemple, si tinguéssim la característica fictícia “té ADN de gat”, dividir per ella produiria subconjunts totalment purs (100% gats a l’esquerra i 0% gats a la dreta).
En general, triem la característica que produeix subconjunts més homogenis.
2. Quan aturar la divisió?
No podem dividir indefinidament. Els criteris típics per aturar la divisió són:
- Puresa total: si un node conté només una classe (100% gats o 100% gossos), es crea una fulla.
- Profunditat màxima: limitem l’arbre a una profunditat determinada.
- La profunditat d’un node és el nombre de salts des de l’arrel.
- Exemple: si imposem una profunditat màxima de 2, cap node pot arribar a profunditat 3.
- Mida mínima del node: si un node té molt poques mostres (p. ex. només 3), es prefereix no dividir més.
- Guany de puresa insuficient: si la millora en puresa (o reducció d’impuresa) és molt petita, no val la pena dividir.
Aquests criteris ajuden a reduir el risc de sobreajustament i a mantenir l’arbre manejable.
Reflexió final
Els arbres de decisió poden semblar complicats perquè, amb els anys, molts investigadors han anat afegint refinaments:
- nous criteris de divisió,
- límits de profunditat,
- criteris de parada alternatius, etc.
Però, en essència, només hi ha dues preguntes clau:
- Quina característica faig servir per dividir?
- Quan em paro de dividir?
Amb aquestes regles, més una bona mesura de puresa (com l’entropia), podem construir arbres de decisió efectius.
Com escollir la millor pregunta?
Quan construïm un arbre de decisió, en cada node hem de decidir quina característica utilitzar per dividir. La intuïció és senzilla: volem preguntes que separin bé els exemples.
Imagina que tens una bossa amb gats i gossos barrejats. Una bona pregunta és aquella que, en respondre-la, et deixa dues bosses on els animals són més semblants entre si (idealment, tots gats a una banda i tots gossos a l’altra).
Mesurar la “barreja”: l’entropia
Per quantificar com de barrejat està un conjunt, fem servir l’entropia:
- Conjunt pur (tots gats o tots gossos) → entropia = 0
- Conjunt 50%-50% → entropia = 1 (màxima confusió)
L’entropia es calcula amb la fórmula H(p)=−plog2(p)−(1−p)log2(1−p), on p és la proporció d’una classe. Però el que importa és la intuïció: com més barrejat, més alta l’entropia.
Exemple: quina característica triem?
Tornem al nostre exemple amb 10 animals (5 gats i 5 gossos). Si provem les tres característiques:
| Característica | Esquerra | Dreta | Resultat |
|---|---|---|---|
| Orelles | 4 gats, 1 gos | 1 gat, 4 gossos | Bona separació |
| Cara | 4 gats, 3 gossos | 1 gat, 2 gossos | Encara barrejats |
| Bigotis | 3 gats, 1 gos | 2 gats, 4 gossos | Regular |
Visualment és clar: “orelles” deixa els grups més purs. Això es reflecteix en el guany d’informació (la reducció d’entropia que aconseguim amb cada divisió):
- Orelles: 0.28 ← màxim guany
- Bigotis: 0.12
- Cara: 0.03
Triem sempre la característica amb el guany més alt.
Criteri d’aturada
El guany d’informació també ens indica quan parar: si el guany és molt petit, no val la pena continuar dividint (només augmentaríem la complexitat de l’arbre sense millorar gaire la precisió).
Nota: Existeixen alternatives a l’entropia, com el criteri de Gini que veurem a continuació. A la pràctica, ambdues mesures donen resultats similars.
Criteri de Gini
El criteri de Gini (o impuresa de Gini) és una altra manera de mesurar com de barrejat està un conjunt. La intuïció és senzilla:
Si agafes dos elements a l’atzar del conjunt, quina probabilitat hi ha que siguin de classes diferents?
- Conjunt pur (tots gats o tots gossos) → Gini = 0 (mai agafaràs dos de classes diferents)
- Conjunt 50%-50% → Gini = 0.5 (màxima barreja)
| Mesura | Rang | Màxim a | Què mesura |
|---|---|---|---|
| Entropia | 0 a 1 | 50%-50% | “Sorpresa” o incertesa |
| Gini | 0 a 0.5 | 50%-50% | Probabilitat d’error aleatori |
Ambdues mesures arriben al mínim (0) quan el conjunt és pur, i al màxim quan hi ha màxima barreja. Per tant, donen resultats molt similars a l’hora d’escollir la millor característica per dividir.
Per què scikit-learn usa Gini per defecte?
- És lleugerament més ràpid de calcular (no requereix logaritmes)
- A la pràctica, la diferència de resultats és mínima
Pots canviar el criteri fàcilment:
from sklearn.tree import DecisionTreeClassifier
# Exemple amb profunditat màxima 3
model = DecisionTreeClassifier(max_depth=3, random_state=42)
# Es podria utilitzar gini o entropy amb:
# model = DecisionTreeClassifier(max_depth=3, random_state=42, criterion='gini')
# model = DecisionTreeClassifier(max_depth=3, random_state=42, criterion='entropy')
model.fit(X_train, y_train)
predictions = model.predict(X_test)
Algorisme de l’arbre de decisió
L’algorisme és recursiu: apliquem el mateix procés a cada node fins que parem.
funció construir_arbre(exemples):
si tots els exemples són de la mateixa classe:
retorna fulla amb aquesta classe
característica = la que té màxim guany d'informació
dividir exemples segons característica
retorna node(
esquerra = construir_arbre(exemples_esquerra),
dreta = construir_arbre(exemples_dreta)
)
Quan parem?
- El node ja és pur (tots de la mateixa classe)
- S’ha arribat a la profunditat màxima
- El guany d’informació és massa petit
- Queden massa pocs exemples per dividir
Les biblioteques com scikit-learn proporcionen valors per defecte raonables per aquests paràmetres.
Codificació One-Hot
Què passa si una característica té més de dos valors? Per exemple, les orelles poden ser punxegudes, caigudes o ovalades.
La solució és crear una columna per cada valor possible:
| Animal | Orelles (original) | Punxegudes | Caigudes | Ovalades | |
|---|---|---|---|---|---|
| Gat 1 | punxegudes | 1 | 0 | 0 | |
| Gat 2 | ovalades | 0 | 0 | 1 | |
| Gos 1 | caigudes | 0 | 1 | 0 |
Això s’anomena one-hot perquè exactament una columna està “encesa” (val 1) per cada fila.
Per què és útil?
Molts algoritmes (xarxes neuronals, regressió lineal/logística) fan operacions matemàtiques amb les dades: multiplicacions, sumes, derivades… Però no podem multiplicar “punxegudes” per un pes. Necessitem números.
La codificació one-hot resol això convertint cada categoria en un vector de 0s i 1s que sí es pot operar matemàticament.
A la pràctica, la majoria de biblioteques ho fan automàticament:
import pandas as pd
# Dades d'exemple
df = pd.DataFrame({
'orelles': ['punxegudes', 'ovalades', 'caigudes']
})
# Codificació one-hot amb pandas
encoded = pd.get_dummies(df, columns=['orelles'])
print(encoded)
# orelles_caigudes orelles_ovalades orelles_punxegudes
# 0 0.0 0.0 1.0
# 1 0.0 1.0 0.0
# 2 1.0 0.0 0.0
Característiques contínues
Fins ara hem vist arbres de decisió amb característiques discretes (orelles punxegudes/caigudes, bigotis sí/no). Però què passa si tenim una característica contínua com el pes de l’animal?
De mitjana, els gats solen ser més lleugers que els gossos. Així doncs, el pes és una característica útil per classificar.
La idea: buscar un llindar
Amb característiques contínues, la pregunta ja no és “té orelles punxegudes?” sinó “pesa menys de X quilos?”. L’algoritme ha de trobar el millor valor de tall.
Exemple: on tallem?
Imaginem que provem diferents llindars:
| Llindar | Esquerra (≤) | Dreta (>) | Qualitat |
|---|---|---|---|
| pes ≤ 8 | 2 gats | 3 gats, 5 gossos | Dolenta (dreta molt barrejada) |
| pes ≤ 9 | 4 gats | 1 gat, 5 gossos | Bona (grups més purs) |
| pes ≤ 13 | 4 gats, 2 gossos | 1 gat, 3 gossos | Regular |
El llindar pes ≤ 9 és el millor: deixa tots els gats lleugers a l’esquerra i gairebé tots els gossos a la dreta.
Com ho fa l’algoritme?
En lloc de provar valors a l’atzar, l’algoritme:
- Ordena els exemples per pes.
- Prova cada punt mitjà entre exemples consecutius com a possible llindar.
- Escull el llindar que produeix els grups més purs (màxim guany d’informació).
Amb 10 exemples, es proven 9 possibles llindars i es queda amb el millor.
Resum
Les característiques contínues es tracten igual que les discretes: l’algoritme busca la divisió que maximitzi la puresa. L’única diferència és que, en lloc de preguntar per categories, pregunta “és menor o igual que X?” per algun valor X que s’ha trobat òptim.
Arbres de decisió per a regressió
Fins ara hem utilitzat arbres de decisió per classificar (gat o gos). Però també poden predir valors numèrics, com ara el pes d’un animal. Això s’anomena regressió.
Què canvia respecte a la classificació?
| Classificació | Regressió | |
|---|---|---|
| Predicció | La classe més freqüent (vot majoritari) | La mitjana dels valors |
| Criteri de divisió | Reduir l’entropia (barreja) | Reduir la variància (dispersió) |
Com funciona?
Imaginem que volem predir el pes d’un animal segons la forma de les orelles i la cara.
- L’arbre divideix els exemples igual que abans.
- A cada fulla, en lloc d’una etiqueta, tenim un conjunt de pesos dels animals d’entrenament.
- La predicció és la mitjana d’aquests pesos.
Exemple: Si una fulla conté animals amb pesos 7.2, 7.6, 10.2 i 8.4 kg, la predicció serà 8.35 kg (la mitjana).
Per què variància en lloc d’entropia?
En classificació, un bon tall separa gats de gossos (redueix la “barreja”).
En regressió, un bon tall agrupa animals amb pesos similars:
- Valors 7, 8, 9 kg → molt agrupats → bona predicció (la mitjana és representativa)
- Valors 5, 12, 20 kg → molt dispersos → mala predicció (la mitjana no representa cap valor real)
L’algoritme busca talls que minimitzin aquesta dispersió (variància) a cada subgrup.
En poques paraules
La mecànica és idèntica a la classificació:
- Dividir segons la característica que més redueixi la variància
- Parar quan el node és prou homogeni o s’arriba al límit
- Predir amb la mitjana dels valors a cada fulla
Hiperparàmetres: controlant la complexitat
Els hiperparàmetres són els “botons de control” que determinen com de complex serà l’arbre. Ajustar-los bé és clau per evitar tant el sobreajustament (arbre massa complex) com el subajustament (arbre massa simple).
Els principals hiperparàmetres
| Hiperparàmetre | Què controla | Efecte si és alt | Efecte si és baix |
|---|---|---|---|
max_depth | Profunditat màxima | Arbre complex, risc de sobreajustament | Arbre simple, risc de subajustament |
min_samples_split | Mínim d’exemples per dividir un node | Divisions més conservatives | Més divisions, arbre més complex |
min_samples_leaf | Mínim d’exemples a cada fulla | Fulles més “segures” | Fulles poden tenir pocs exemples |
La intuïció: profunditat i sobreajustament
Imagina un arbre amb profunditat il·limitada:
- Pot créixer fins que cada fulla contingui un sol exemple
- Aconseguirà 100% accuracy en entrenament (memoritza les dades)
- Però fallarà amb dades noves (no ha après patrons generals)
És com estudiar un examen memoritzant les respostes exactes en lloc d’entendre els conceptes.
Exemple pràctic:
| Profunditat | Train accuracy | Test accuracy | Diagnòstic |
|---|---|---|---|
| 2 | 75% | 74% | Subajustament (massa simple) |
| 5 | 92% | 88% | Bon equilibri |
| 20 | 100% | 72% | Sobreajustament (memoritza) |
Com trobar els valors òptims?
La millor estratègia és validació creuada: provar diferents combinacions i veure quina funciona millor amb dades de validació.
La idea és senzilla: dividim les dades en k parts (típicament 5). Entrenem el model k vegades, cada vegada deixant una part diferent per validar. Així obtenim k mesures de rendiment que podem fer la mitjana.
Per què és millor que una sola divisió train/test?
- Amb una sola divisió, el resultat depèn de quins exemples han quedat a cada costat (sort)
- Amb k divisions rotatives, cada exemple serveix tant per entrenar com per validar
- El resultat és més fiable i estable, especialment amb datasets petits
Per una explicació més detallada, consulta la secció K-Fold Cross-Validation.
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import GridSearchCV
# Definir el rang de valors a provar
param_grid = {
'max_depth': [3, 5, 10, 20, None],
'min_samples_split': [2, 5, 10],
'min_samples_leaf': [1, 2, 4]
}
# Cercar la millor combinació (cv=5 significa k=5 folds)
tree = DecisionTreeClassifier(random_state=42)
search = GridSearchCV(tree, param_grid, cv=5, scoring='accuracy')
search.fit(X_train, y_train)
print(f"Millors paràmetres: {search.best_params_}")
print(f"Millor score: {search.best_score_:.3f}")
Consells pràctics
- Comença simple:
max_depth=5és un bon punt de partida - Observa la diferència train/test: si train >> test, l’arbre és massa complex
- Per datasets petits: limita més la profunditat (menys dades = més risc de sobreajustar)
Nota sobre poda (pruning): Existeix una tècnica alternativa anomenada post-pruning, que deixa créixer l’arbre completament i després talla branques innecessàries. A la pràctica, controlar la complexitat amb hiperparàmetres (com fem aquí) és més comú i sol ser suficient. Si necessites simplificar un arbre ja entrenat, scikit-learn ofereix el paràmetre
ccp_alpha.
Importància de les característiques
Un dels grans avantatges dels arbres de decisió és que ens diuen quines característiques són més útils per fer prediccions. Això s’anomena feature importance (importància de les característiques), i mesura quanta impuresa elimina una característica en el total de l’arbre.
La intuïció
Recorda que a cada node l’arbre escull la característica que més redueix la impuresa (entropia o Gini). Si una característica:
- S’usa a prop de l’arrel → afecta molts exemples → és molt important
- S’usa només a les fulles → afecta pocs exemples → és menys important
- No s’usa mai → importància = 0
Exemple pràctic
Tornem al nostre classificador de gats. Després d’entrenar, podem veure la importància de cada característica:
| Característica | Importància |
|---|---|
| Forma orelles | 0.52 |
| Bigotis | 0.31 |
| Forma cara | 0.17 |
Això ens diu que la forma de les orelles és el factor més determinant per distingir gats de gossos en les nostres dades.
Com obtenir-ho amb codi
from sklearn.tree import DecisionTreeClassifier
import pandas as pd
# Entrenar el model
model = DecisionTreeClassifier(max_depth=5, random_state=42)
model.fit(X_train, y_train)
# Obtenir la importància de cada característica
importances = pd.DataFrame({
'característica': feature_names,
'importància': model.feature_importances_
}).sort_values('importància', ascending=False)
print(importances)
Per a què serveix?
- Entendre el model: saber què mira l’arbre per decidir
- Explicar prediccions: “et classifiquem com a risc alt principalment pel teu historial de crèdit”
- Selecció de característiques: eliminar les que tenen importància zero per simplificar
- Detectar problemes: si una característica inesperada és molt important, potser hi ha un error a les dades
Visualitzar l’arbre
També pots dibuixar l’arbre complet per veure exactament quines decisions pren:
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
plt.figure(figsize=(15, 8))
plot_tree(
model,
feature_names=feature_names,
class_names=['gos', 'gat'],
filled=True,
rounded=True
)
plt.show()
Nota: La visualització només és útil per arbres petits. Amb
max_depth > 5, l’arbre es fa difícil de llegir.
Conjunts d’arbres (Ensembles)
Un ensemble és fer treballar molts models junts per obtenir millors resultats. En lloc de confiar en un sol arbre de decisió, entrenem molts arbres i els fem votar.
Per què un sol arbre no és suficient?
Un arbre de decisió és molt sensible a petits canvis en les dades. Si canviem un sol exemple del conjunt d’entrenament, la característica escollida al node arrel pot canviar, generant un arbre totalment diferent.
La solució: entrenar molts arbres diferents i combinar les seves prediccions. Així, cap arbre individual té massa influència sobre el resultat final.
Com funciona la votació?
Imaginem un ensemble de 3 arbres classificant un animal:
| Arbre | Predicció |
|---|---|
| Arbre 1 | gat |
| Arbre 2 | gos |
| Arbre 3 | gat |
Resultat: 2 vots gat, 1 vot gos → gat guanya per majoria.
Com creem arbres diferents?
Si entrenem tots els arbres amb les mateixes dades, obtindrem arbres idèntics. Necessitem variació. Hi ha dues tècniques:
Bagging (mostreig amb reposició)
Per cada arbre, creem un conjunt d’entrenament lleugerament diferent:
- Posem tots els exemples en una “bossa”
- Traiem exemples a l’atzar, tornant-los a posar cada vegada
- Repetim fins tenir el mateix nombre d’exemples
El resultat: alguns exemples es repeteixen, altres no apareixen.
| Dades originals | Mostra 1 | Mostra 2 | Mostra 3 |
|---|---|---|---|
| A, B, C, D, E | A, A, C, D, E | B, C, C, D, E | A, B, D, D, E |
Selecció aleatòria de característiques
A cada node, en lloc de considerar totes les característiques, només en considerem un subconjunt aleatori (típicament √n). Això força els arbres a explorar camins diferents.
Random Forest
Random Forest combina ambdues tècniques:
- Crear ~100 arbres, cadascun entrenat amb un mostreig diferent de les dades
- A cada node, considerar només un subconjunt aleatori de característiques
- Per predir: cada arbre vota, guanya la majoria
Això produeix arbres diversos que, combinats, són molt més robustos que un sol arbre.
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=42)
rf.fit(X_train, y_train)
predictions = model.predict(X_test)
XGBoost (Boosting)
XGBoost utilitza una estratègia diferent: en lloc d’arbres independents, cada arbre corregeix els errors dels anteriors.
La idea és com la pràctica deliberada al piano: en lloc de tocar tota la peça repetidament, et concentres en els compassos que encara no domines.
| Pas | Què fa |
|---|---|
| 1 | Entrenar el primer arbre normalment |
| 2 | Identificar els exemples mal classificats |
| 3 | Entrenar el següent arbre donant més pes als errors |
| 4 | Repetir fins tenir ~100 arbres |
Random Forest vs XGBoost
| Random Forest | XGBoost | |
|---|---|---|
| Idea | Arbres independents que voten | Arbres que corregeixen errors anteriors |
| Entrenament | Paral·lel (més ràpid) | Seqüencial |
| Quan usar | Bon punt de partida | Quan necessites màxima precisió |
A la pràctica, XGBoost sol donar millors resultats i és l’algoritme dominant en competicions de ML i aplicacions comercials.
from xgboost import XGBClassifier
# Classificació
model = XGBClassifier(n_estimators=100, max_depth=5, random_state=42)
model.fit(X_train, y_train)
predictions = model.predict(X_test)
# Per regressió: usar XGBRegressor amb els mateixos paràmetres
Quan usar arbres vs xarxes neuronals?
| Arbres (XGBoost) | Xarxes neuronals | |
|---|---|---|
| Dades tabulars (fulls de càlcul) | Recomanat | Funciona |
| Imatges, àudio, text | No adequat | Recomanat |
| Velocitat d’entrenament | Ràpid | Lent |
| Interpretabilitat | Alta (arbres petits) | Baixa |
| Transfer learning | No | Sí |
| Dataset petit | Funciona bé | Necessita més dades |
Recomanació pràctica
- Dades en taules (preus, classificacions, prediccions numèriques): comença amb XGBoost
- Imatges, vídeo, àudio, text: usa xarxes neuronals
- Si tens dubtes amb dades tabulars, prova ambdós i compara